problem 1.
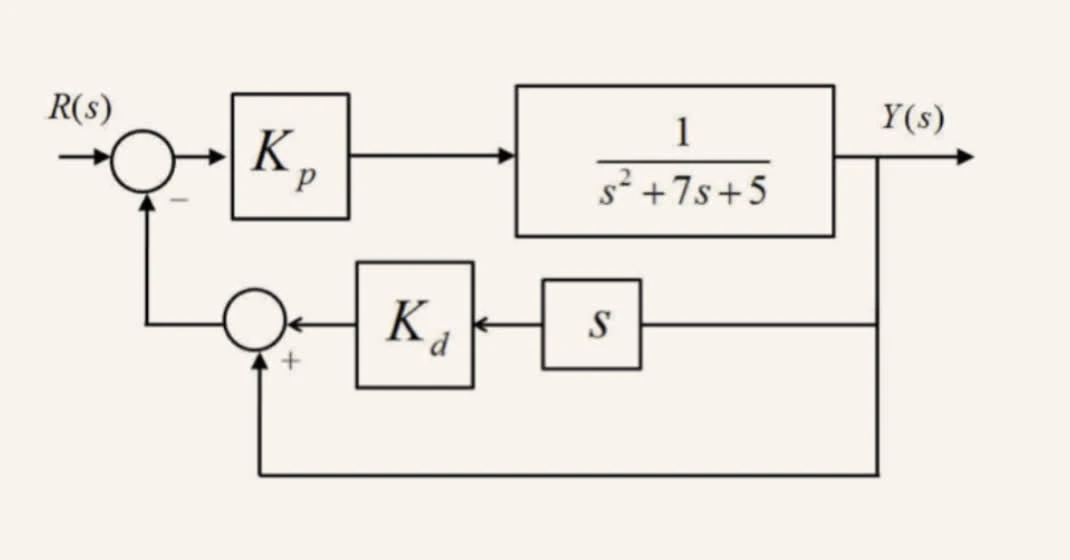
Consider the following system:
Question
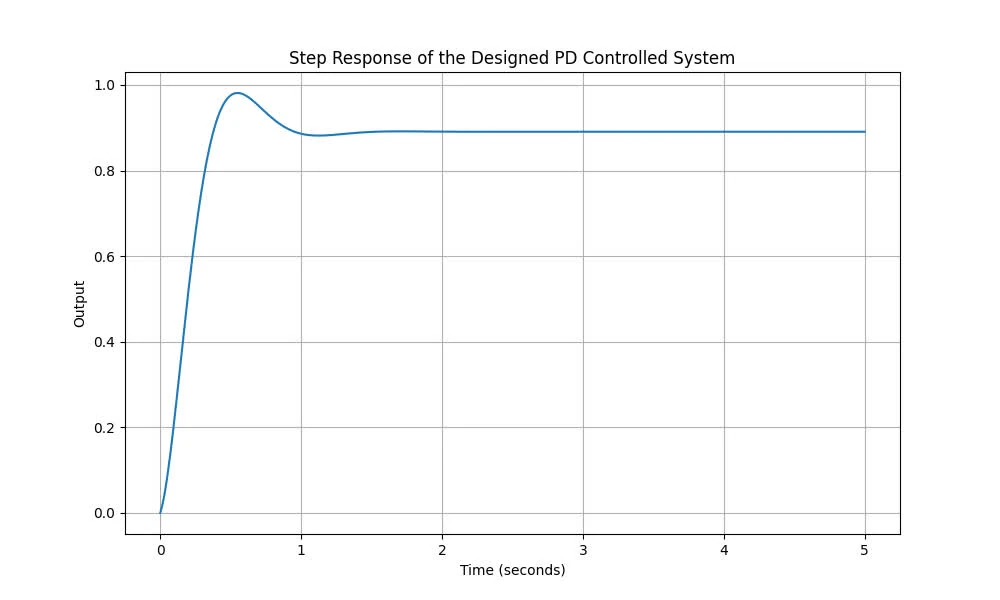
Using the properties of second-order systems, determine and such that the overshoot is 10 percent and the settling time is 1 second. Confirm that your design meets the requirements by plotting the step response.
Given the percent overshoot and settling time based on the damping ratio and natural frequency :
For 10% overshoot, we can solve for : . For 1 second settling time, we can solve for : .
Given second-order systems’ transfer function:
and the transfer function of the PID controller in the given system is given by:
The transfer function is then followed by:
We then have and to solve for and :
Thus, and .
The following is the code snippet for generating the graphs and results:
from scipy.optimize import fsolve
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import TransferFunction, step
OS, Ts = 0.10, 1.0
zeta = fsolve(lambda z: np.exp(-z*np.pi/np.sqrt(1-z**2)) - OS, 0.5)[0]
wn = 4 / (zeta * Ts)
# Coefficients from the standard second-order system
a1 = 2 * zeta * wn # coefficient of s
a0 = wn**2 # constant coefficient
# Equating the coefficients to solve for Kp and Kd
# 7 + Kd = a1 and 5 + Kp = a0
Kd = a1 - 7
Kp = a0 - 5
# Confirm the design by plotting the step response
# First, define the transfer function of the closed-loop system with the calculated Kp and Kd
G = TransferFunction([Kd, Kp], [1, 7+Kd, 5+Kp])
# Now, generate the step response of the system
time = np.linspace(0, 5, 500)
time, response = step(G, T=time)
print(Kp, Kd, zeta, wn)
# Plot the step response
plt.figure(figsize=(10, 6))
plt.plot(time, response)
plt.title('Step Response of the Designed PD Controlled System')
plt.xlabel('Time (seconds)')
plt.ylabel('Output')
plt.grid(True)
plt.show()problem 2.
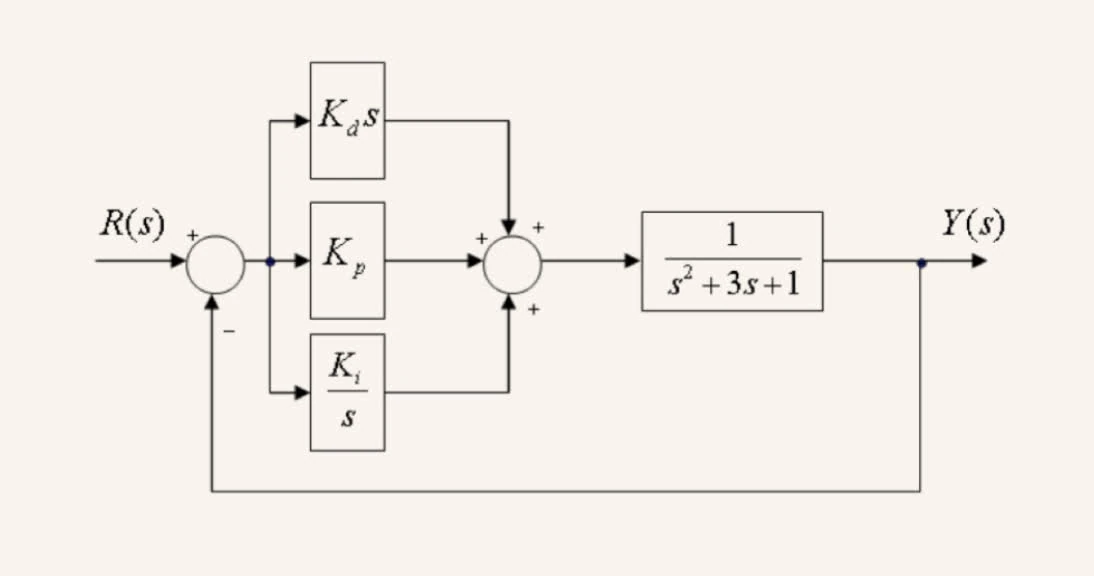
Consider the following system:
set a.
If , is the system stable? (Please determine this by explicitly finding the poles of the closed-loop system and reasoning about stability based on the pole locations.)
Given that , The PID controller transfer function is:
The open-loop transfer function is given by: .
Thus the closed-loop transfer function is given by .
We need to solve to find the poles of the closed-loop system.
import numpy as np
print(np.roots([1,1,4,2]))which yields [-0.23341158+1.92265955j -0.23341158-1.92265955j -0.53317683+0.j] as poles. Since all the poles have negative real parts, the system is stable.
set b.
Fix . Using the Routh-Hurwitz criterion, determine the ranges of and that result in a stable system.
The open-loop transfer function is given by
The characteristic equation of the closed-loop system is given by :
Applying the Routh-Hurwitz criterion, we have the following table:
from sympy import symbols, Matrix
Kd, Kp = symbols('Kd Kp')
a0 = 10
a1 = Kp + 1
a2 = 3 + Kd
a3 = 1
routh = Matrix([
[a3, a1],
[a2, a0],
[a1 - (a2*a3)/a3, 0],
[a0, 0]
])
print(routh)which results in the following table:
Matrix([[1, Kp + 1], [Kd + 3, 10], [-Kd + Kp - 2, 0], [10, 0]])The conditions for stability from the Routh-Hurwitz criterion states that all the elements in the first column of the Routh array must be positive. Thus, we have the following inequalities:
Solving for and yields the following ranges:
set c.
For the system in the first question, suppose that you want the steady-state error to be . What should the values of and be? (Hint: the system is not in the unity gain form that we discussed in detail in lecture, so be careful.)
The open-loop transfer function is given by:
The transfer function for closed-loop is given by:
From final value theorem, the steady-state error is given by
For step input we got