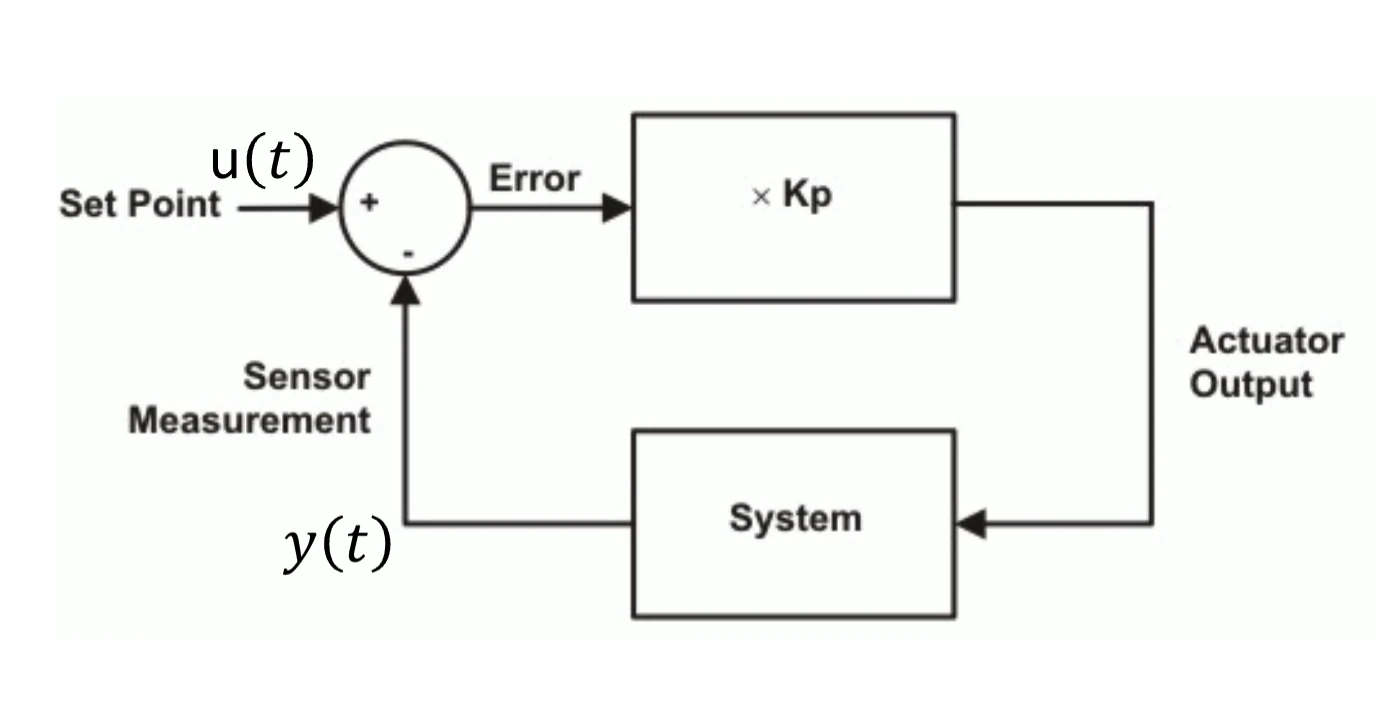
PID controller proportional control
K p e ( t ) = K p [ u ( t ) − y ( t ) ] K_p e(t) = K_p [u(t) - y(t)] K p e ( t ) = K p [ u ( t ) − y ( t )]
Example: Given the closed-loop transfer function is T ( s ) = G p ( s ) 1 + G p ( s ) = 1 s + 2 T(s) = \frac{G_p(s)}{1+G_p(s)} = \frac{1}{s+2} T ( s ) = 1 + G p ( s ) G p ( s ) = s + 2 1
adding proportional closed-loop transfer function is:
T ( s ) = K p G p 1 + K p G p T(s) = \frac{K_p G_p}{1 + K_p G_p} T ( s ) = 1 + K p G p K p G p integral control "\\usepackage{tikz}\n\\usetikzlibrary{positioning, arrows.meta}\n\n\\begin{document}\n\\begin{tikzpicture}[auto, node distance=2cm, >=Latex, block/.style={draw, minimum width=1.5cm, minimum height=1cm}]\n\n% Nodes\n\\node[draw, circle, minimum size=0.5cm] (sum) {}; % Summing junction\n\\node[block, right=2cm of sum] (compensator) {$\\frac{K_I}{s}$};\n\\node[block, right=2.5cm of compensator] (Gp) {$\\frac{1}{s+1}$};\n\\node[below=1.5cm of compensator] (feedback) {feedback};\n\n% Labels\n\\node[above=0.1cm of compensator] {compensator};\n\\node[above=0.1cm of Gp] {$G_p(s)$};\n\n% Input and Output\n\\node[left=1cm of sum] (input) {R(s)};\n\\node[right=1cm of Gp] (output) {C(s)};\n\n% Arrows (Forward path)\n\\draw[->] (input) -- (sum.west);\n\\draw[->] (sum.east) -- (compensator.west);\n\\draw[->] (compensator.east) -- (Gp.west);\n\\draw[->] (Gp.east) -- (output);\n\n% Feedback path\n\\draw[->] (output.east) -- ++(1,0) |- (feedback) -| (sum.south);\n\n% Plus and Minus signs\n\\node at (0.2, 0.5) {$+$};\n\\node at (0.2, -0.5) {$-$};\n\n\\end{tikzpicture}\n\\end{document}" K I s 1 s +1 feedbac k comp ensator G p ( s ) R(s) C(s) + ¡ source code Closed loop here yields
T ( s ) = K I s 2 + s + K I T(s) = \frac{K_I}{s^2 + s + K_I} T ( s ) = s 2 + s + K I K I steady state error is 0, while steady-state output is 1
PI control proportional-integral
"\\usepackage{tikz}\n\\usetikzlibrary{positioning, arrows.meta}\n\n\\begin{document}\n\\begin{tikzpicture}[auto, node distance=2cm, >=Latex, block/.style={draw, minimum width=1.5cm, minimum height=1cm}]\n\n% Nodes\n\\node[draw, circle, minimum size=0.5cm] (sum) {}; % Summing junction\n\\node[block, right=2cm of sum] (compensator) {$G_c = \\frac{K_I}{s} + K_p$};\n\\node[block, right=2.5cm of compensator] (Gp) {$\\frac{1}{s+1}$};\n\\node[below=1.5cm of compensator] (feedback) {feedback};\n\n% Labels\n\\node[above=0.1cm of compensator] {compensator};\n\\node[above=0.1cm of Gp] {$G_p(s)$};\n\n% Input and Output\n\\node[left=1cm of sum] (input) {R(s)};\n\\node[right=1cm of Gp] (output) {C(s)};\n\n% Arrows (Forward path)\n\\draw[->] (input) -- (sum.west);\n\\draw[->] (sum.east) -- (compensator.west);\n\\draw[->] (compensator.east) -- (Gp.west);\n\\draw[->] (Gp.east) -- (output);\n\n% Feedback path\n\\draw[->] (output.east) -- ++(1,0) |- (feedback) -| (sum.south);\n\n% Plus and Minus signs\n\\node at (0.2, 0.5) {$+$};\n\\node at (0.2, -0.5) {$-$};\n\n\\end{tikzpicture}\n\\end{document}" G c = K I s + K p 1 s +1 feedbac k comp ensator G p ( s ) R(s) C(s) + ¡ source code Closed-loop transfer function
T ( s ) = K I + s K p s 2 + ( 1 + K p ) s + K I T(s) = \frac{K_I + sK_p}{s^{2} + (1+K_p)s + K_I} T ( s ) = s 2 + ( 1 + K p ) s + K I K I + s K p
PC: impact on speed of response
IC: force steady-state error to 0
derivative control "\\usepackage{tikz}\n\\usetikzlibrary{positioning, arrows.meta}\n\n\\begin{document}\n\\begin{tikzpicture}[auto, node distance=2cm, >=Latex, block/.style={draw, minimum width=1.5cm, minimum height=1cm}]\n\n% Nodes\n\\node[draw, circle, minimum size=0.5cm] (sum) {}; % Summing junction\n\\node[block, right=2cm of sum] (compensator) {$G_c = K_D s$};\n\\node[block, right=2.5cm of compensator] (Gp) {$\\frac{1}{s+1}$};\n\\node[below=1.5cm of compensator] (feedback) {feedback};\n\n% Labels\n\\node[above=0.1cm of compensator] {compensator};\n\\node[above=0.1cm of Gp] {$G_p(s)$};\n\n% Input and Output\n\\node[left=1cm of sum] (input) {R(s)};\n\\node[right=1cm of Gp] (output) {C(s)};\n\n% Arrows (Forward path)\n\\draw[->] (input) -- (sum.west);\n\\draw[->] (sum.east) -- (compensator.west);\n\\draw[->] (compensator.east) -- (Gp.west);\n\\draw[->] (Gp.east) -- (output);\n\n% Feedback path\n\\draw[->] (output.east) -- ++(1,0) |- (feedback) -| (sum.south);\n\n% Plus and Minus signs\n\\node at (0.2, 0.5) {$+$};\n\\node at (0.2, -0.5) {$-$};\n\n\\end{tikzpicture}\n\\end{document}" G c = K D s 1 s +1 feedbac k comp ensator G p ( s ) R(s) C(s) + ¡ source code T ( s ) = K D s ( 1 + K D ) s + 1 T(s) = \frac{K_D s}{(1+K_D)s + 1} T ( s ) = ( 1 + K D ) s + 1 K D s
introduces an open-loop zero
K D K_D K D
T ( s ) = s K D P ω n 2 s 2 + 2 ( ζ + K D 2 P ω n ) ω n s + ω n 2 T(s) = \frac{s K_D P \omega_n^2}{s^{2}+ 2(\zeta + \frac{K_D}{2} P\omega_n)\omega_n s + \omega_n^2} T ( s ) = s 2 + 2 ( ζ + 2 K D P ω n ) ω n s + ω n 2 s K D P ω n 2 damping effect ζ ′ = ζ + K D 2 P ω n \zeta^{'} = \zeta + \frac{K_D}{2}P\omega_n ζ ′ = ζ + 2 K D P ω n
PID control G C ( s ) = K p + K I s + K D s G_C(s) = K_p + \frac{K_I}{s} + K_D s G C ( s ) = K p + s K I + K D s in time domain:
u ( t ) = K P e ( t ) + K I ∫ 0 t e ( η ) d η + K D d ( e ( t ) ) d t u(t) = K_P e(t) + K_I \int_{0}^{t} e(\eta) d\eta + K_D \frac{d(e(t))}{dt} u ( t ) = K P e ( t ) + K I ∫ 0 t e ( η ) d η + K D d t d ( e ( t )) Component Discrete-Time Equation Proportional u ( k ) = K P e ( k ) u(k) = K_P e(k) u ( k ) = K P e ( k ) Integral u ( k ) = K I T ∑ i = 1 k e ( i ) u(k) = K_I T \sum_{i=1}^{k} e(i) u ( k ) = K I T ∑ i = 1 k e ( i ) Derivative u ( k ) = K D T [ e ( k ) − e ( k − 1 ) ] u(k) = \frac{K_D}{T}[e(k) - e(k-1)] u ( k ) = T K D [ e ( k ) − e ( k − 1 )]
approximate of PID controller: u ( k ) = K P e ( k ) + K I T ∑ i = 1 n e ( i ) + K D T [ e ( k ) − e ( k − 1 ) ] u(k) = K_P e(k) + K_I T \sum_{i=1}^{n} e(i) + \frac{K_D}{T}[e(k) - e(k-1)] u ( k ) = K P e ( k ) + K I T ∑ i = 1 n e ( i ) + T K D [ e ( k ) − e ( k − 1 )]