Real-time control systems, and scheduling see also
time domain versus frequency domain use Laplace transform to convert from time domain to frequency domain
Consider the following circuit:
RC d v o ( t ) d t + v o ( t ) = v i ( t ) v i ( t ) = 1 \begin{aligned}
\text{RC} \frac{d v_o(t)}{dt} + v_o(t) &= v_i(t) \\
v_i(t) &= 1
\end{aligned} RC d t d v o ( t ) + v o ( t ) v i ( t ) = v i ( t ) = 1 graph LR
Diff{{differential equations}} -- "Laplace transform" --> Algebraic{{algebraic equations}} -- "inverse Laplace transform" --> End{{time domain solution}}L { f ( t ) } = ∫ 0 ∞ f ( t ) − s t d t = F ( s ) \mathcal{L} \{f(t)\} = \int_0^{\infty}f(t)^{-st}dt = F(s) L { f ( t )} = ∫ 0 ∞ f ( t ) − s t d t = F ( s ) Item no. f ( t ) F ( s ) 1. δ ( t ) 1 2. u ( t ) 1 s 3. t u ( t ) 1 s 2 4. t n u ( t ) n ! s n + 1 5. e − a t u ( t ) 1 s + a 6. sin ( ω t ) u ( t ) ω s 2 + ω 2 7. cos ( ω t ) u ( t ) s s 2 + ω 2 \begin{array}{c c c} \hline \text{Item no.} & f(t) & F(s) \\ \hline 1. & \delta(t) & 1 \\ 2. & u(t) & \frac{1}{s} \\ 3. & tu(t) & \frac{1}{s^2} \\ 4. & t^n u(t) & \frac{n!}{s^{n+1}} \\ 5. & e^{-at}u(t) & \frac{1}{s + a} \\ 6. & \sin(\omega t)u(t) & \frac{\omega}{s^2 + \omega^2} \\ 7. & \cos(\omega t)u(t) & \frac{s}{s^2 + \omega^2} \\ \hline \end{array} Item no. 1. 2. 3. 4. 5. 6. 7. f ( t ) δ ( t ) u ( t ) t u ( t ) t n u ( t ) e − a t u ( t ) sin ( ω t ) u ( t ) cos ( ω t ) u ( t ) F ( s ) 1 s 1 s 2 1 s n + 1 n ! s + a 1 s 2 + ω 2 ω s 2 + ω 2 s δ ( t ) = 0 , t ≠ 0 , ∫ 0 ∞ δ ( t ) d t = 1 \delta{(t)} = 0, \quad t \neq 0,\quad \int_0^{\infty}{\delta{(t)}}dt=1 δ ( t ) = 0 , t = 0 , ∫ 0 ∞ δ ( t ) d t = 1 example: Given a unit step function u ( t ) = { 0 t < 0 1 t ≥ 0 u(t) = \begin{cases} 0 & t < 0 \\ 1 & t \ge 0 \end{cases} u ( t ) = { 0 1 t < 0 t ≥ 0
U ( s ) = L { u ( t ) } = ∫ 0 ∞ u ( t ) e − s t d t = − 1 s e − s t d t U ( s ) = − 1 s ( 0 − 1 ) = 1 s \begin{aligned}
U(s) = \mathcal{L} \{u(t)\} &= \int_{0}^{\infty} u(t) e^{-st} dt = -\frac{1}{s} e^{-st} dt \\
U(s) &= -\frac{1}{s}(0-1) = \frac{1}{s}
\end{aligned} U ( s ) = L { u ( t )} U ( s ) = ∫ 0 ∞ u ( t ) e − s t d t = − s 1 e − s t d t = − s 1 ( 0 − 1 ) = s 1 L − 1 { F ( s ) } = 1 2 π j lim ω → ∞ ∫ σ − j ω σ + j ω F ( s ) e s t d s \mathcal{L}^{-1} \{ F(s) \} = \frac{1}{2\pi j} \lim_{\omega \to \infty} \int_{\sigma-j\omega}^{\sigma+j\omega} F(s) e^{st} \, ds L − 1 { F ( s )} = 2 πj 1 ω → ∞ lim ∫ σ − jω σ + jω F ( s ) e s t d s
if L [ f ( t ) ] = F ( s ) \mathcal{L}[f(t)] = F(s) L [ f ( t )] = F ( s )
L [ f ′ ( t ) ] = s F ( s ) − f ( 0 ) L [ ∫ 0 t f ( t ) d t ] = F ( s ) s \begin{aligned}
\mathcal{L}[f^{'}(t)] &= sF(s) -f(0) \\
\mathcal{L}[\int_0^{t}f(t) dt] &= \frac{F(s)}{s}
\end{aligned} L [ f ′ ( t )] L [ ∫ 0 t f ( t ) d t ] = s F ( s ) − f ( 0 ) = s F ( s )
For higher derivatives we have L [ f ′ ′ ( t ) ] = s 2 F ( s ) − s f ( 0 ) − f ′ ( 0 ) \mathcal{L}[f^{''}(t)] = s^{2} F(s) - sf(0) - f^{'}(0) L [ f ′′ ( t )] = s 2 F ( s ) − s f ( 0 ) − f ′ ( 0 )
we can replace s s s j w jw j w
ex: G ( j w ) = 1 1 + j w RC G(jw) = \frac{1}{1+jw \text{RC}} G ( j w ) = 1 + j w RC 1 ∣ G ( j w ) ∣ = ∣ 1 1 + j w RC ∣ = 1 1 + ( w RC 2 ) |G(jw)| = |\frac{1}{1+jw \text{RC}}| = \frac{1}{\sqrt{1+(w \text{RC}^2)}} ∣ G ( j w ) ∣ = ∣ 1 + j w RC 1 ∣ = 1 + ( w RC 2 ) 1
reasoning: we substitute Laplace transform with s = j w s=jw s = j w
example for a first-order system
Y ( s ) = s + 2 s ( s + 5 ) = 2 5 s + 3 5 ( s + 5 ) y ( t ) = 2 5 + 3 5 e − 5 t ∵ total response = forced + natural \begin{aligned}
Y(s) &= \frac{s+2}{s(s+5)} = \frac{2}{5s} + \frac{3}{5(s+5)} \\
y(t) &= \frac{2}{5} + \frac{3}{5} e^{-5t} \\[8pt]
\because \text{total response} &= \text{forced} + \text{natural}
\end{aligned} Y ( s ) y ( t ) ∵ total response = s ( s + 5 ) s + 2 = 5 s 2 + 5 ( s + 5 ) 3 = 5 2 + 5 3 e − 5 t = forced + natural stability: total response = natural response + forced response
the output response of a system
natural (transient ) response: 3 5 e − 5 t \frac{3}{5} e^{-5t} 5 3 e − 5 t
forced response (steady-state ) response: 2 5 \frac{2}{5} 5 2
poles and zeros zeros and poles generate the amplitude for both forced and natural response
Y ( s ) = s + 2 s ( s + 5 ) Y(s) = \frac{s+2}{s(s+5)} Y ( s ) = s ( s + 5 ) s + 2 s = 0 , − 5 s=0,-5 s = 0 , − 5 s = − 2 s=-2 s = − 2
at origin, generated step function
at -5 generate transient response e − 5 t e^{-5t} e − 5 t
We will consider first-order and second-order system
first-order systems, time constant "\\usepackage{tikz}\n\\usetikzlibrary{positioning}\n\n\\begin{document}\n\\begin{tikzpicture}[auto, node distance=2cm, >=latex]\n\n% Nodes\n\\node[draw, rectangle, minimum width=3cm, minimum height=1.5cm] (block) {$\\frac{a}{s + a}$};\n\\node[left=1.5cm of block] (input) {$X(s) = \\frac{1}{s}$};\n\\node[right=1.5cm of block] (output) {$Y(s)$};\n\\node[above=0.5cm of block] (G) {$G(s)$};\n\n% Arrows\n\\draw[->] (input) -- (block);\n\\draw[->] (block) -- (output);\n\n\\end{tikzpicture}\n\\end{document}" a s + a X ( s ) = 1 s Y ( s ) G ( s ) source code Output of a general first-order system is
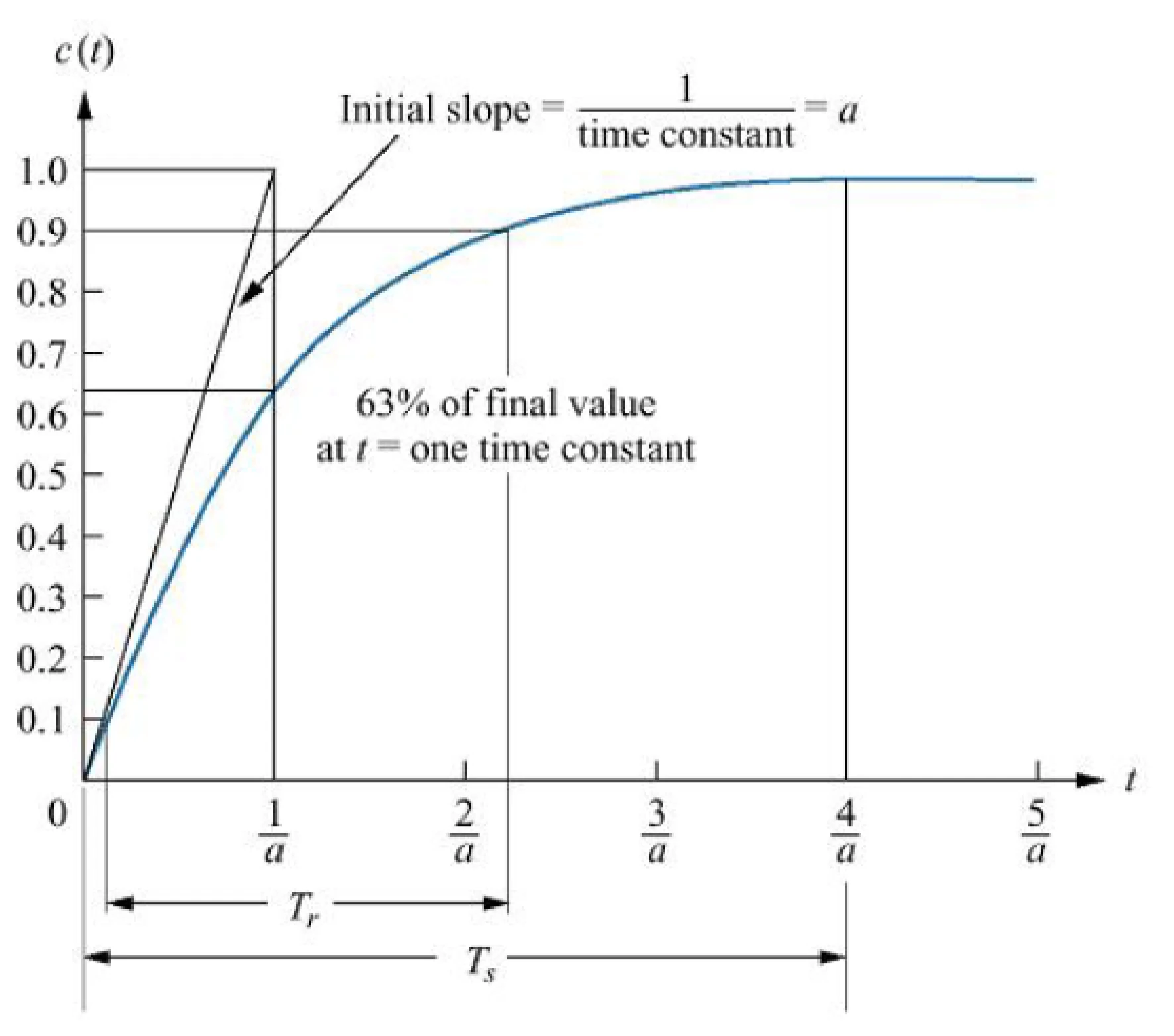
Y ( s ) = X ( s ) G ( s ) = a s ( s + a ) Y(s) = X(s)G(s) = \frac{a}{s(s+a)} Y ( s ) = X ( s ) G ( s ) = s ( s + a ) a thus the time domain output is y ( t ) = 1 − e − a t y(t) = 1 - e^{-at} y ( t ) = 1 − e − a t
usually, t = 1 a t=\frac{1}{a} t = a 1 y ( t ) = 0.63 y(t) = 0.63 y ( t ) = 0.63
response in time domain
T r T_r T r
for first order: T r = 2.2 a T_r = \frac{2.2}{a} T r = a 2.2
T s T_s T s
for first order: T s = 4 a T_s = \frac{4}{a} T s = a 4
second-order systems general order system:
G ( s ) = b s 2 + a s + b G(s) = \frac{b}{s^{2}+as +b} G ( s ) = s 2 + a s + b b Thus the pole for this system:
s 1 , s 2 = − a + a 2 − 4 b 2 s_{1},s_{2}= \frac{-a + \sqrt{a^2 - 4b}}{2} s 1 , s 2 = 2 − a + a 2 − 4 b natural frequency happens when a = 0 a=0 a = 0
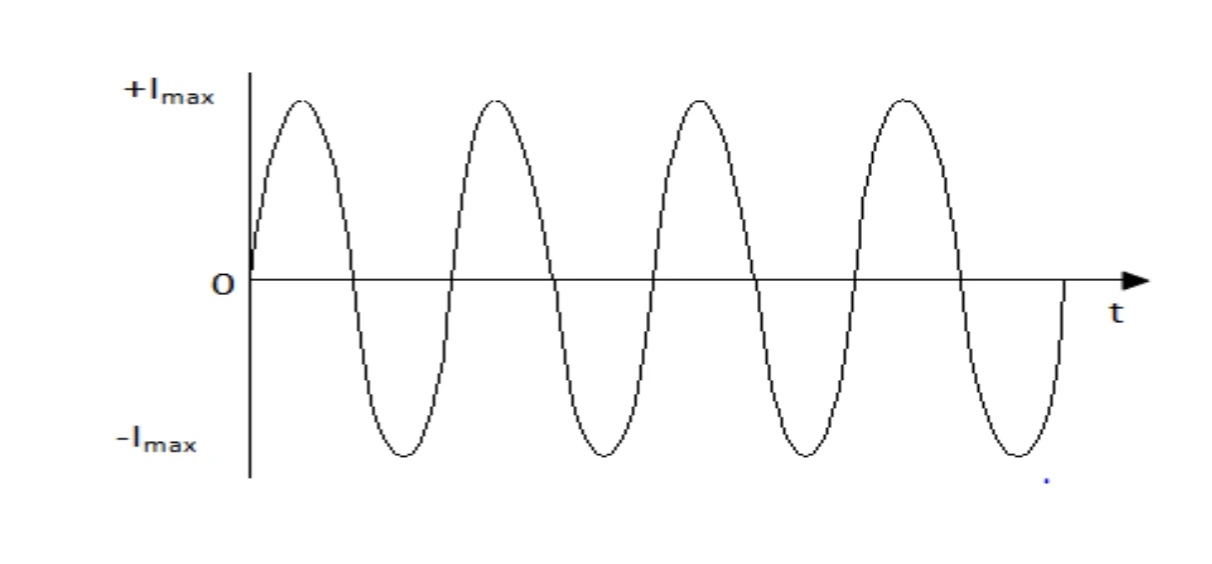
The transfer function is G ( s ) = b s 2 + b G(s)=\frac{b}{s^{2}+b} G ( s ) = s 2 + b b ± j w \pm jw ± j w
w n = b w_n = \sqrt{b} w n = b
in a sense, this is the undamped case:
damping coefficient complex poles has real part σ = − a 2 \sigma = -\frac{a}{2} σ = − 2 a
damping ratio is defined as:
ζ = exponential decay frequency natural frequency = ∣ σ ∣ w n \zeta = \frac{\text{exponential decay frequency}}{\text{natural frequency}} = \frac{|\sigma|}{w_n} ζ = natural frequency exponential decay frequency = w n ∣ σ ∣
So that a = 2 ζ w n a = 2 \zeta w_n a = 2 ζ w n
general second order G ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 s 1 , s 2 = − ζ w n ± w n ζ 2 − 1 \begin{aligned}
G(s) &= \frac{w_n^2}{s^2 + 2 \zeta w_n s + w_n^2} \\[12pt]
s_{1},s_{2} &= - \zeta w_n \pm w_n \sqrt{\zeta^2 - 1}
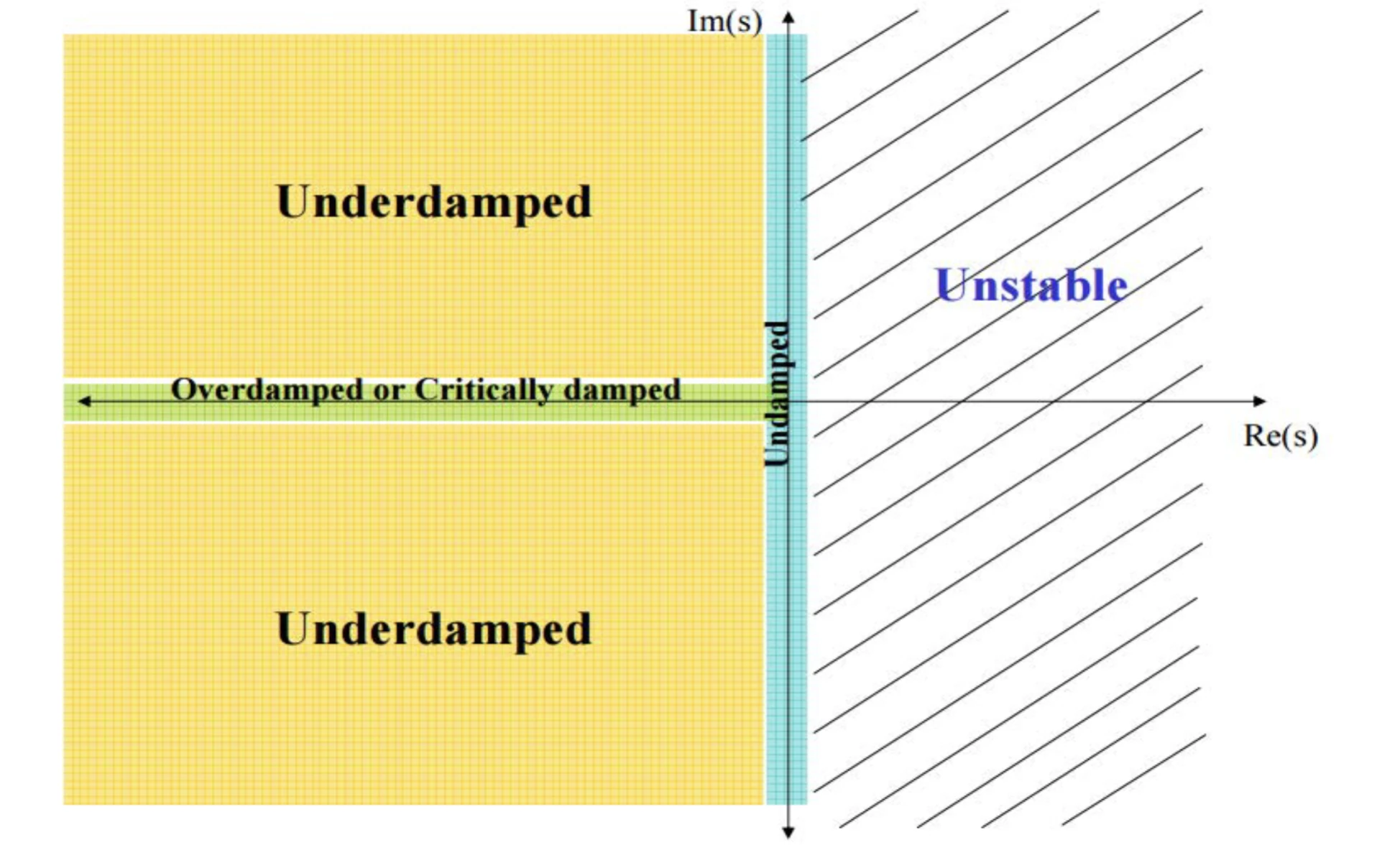
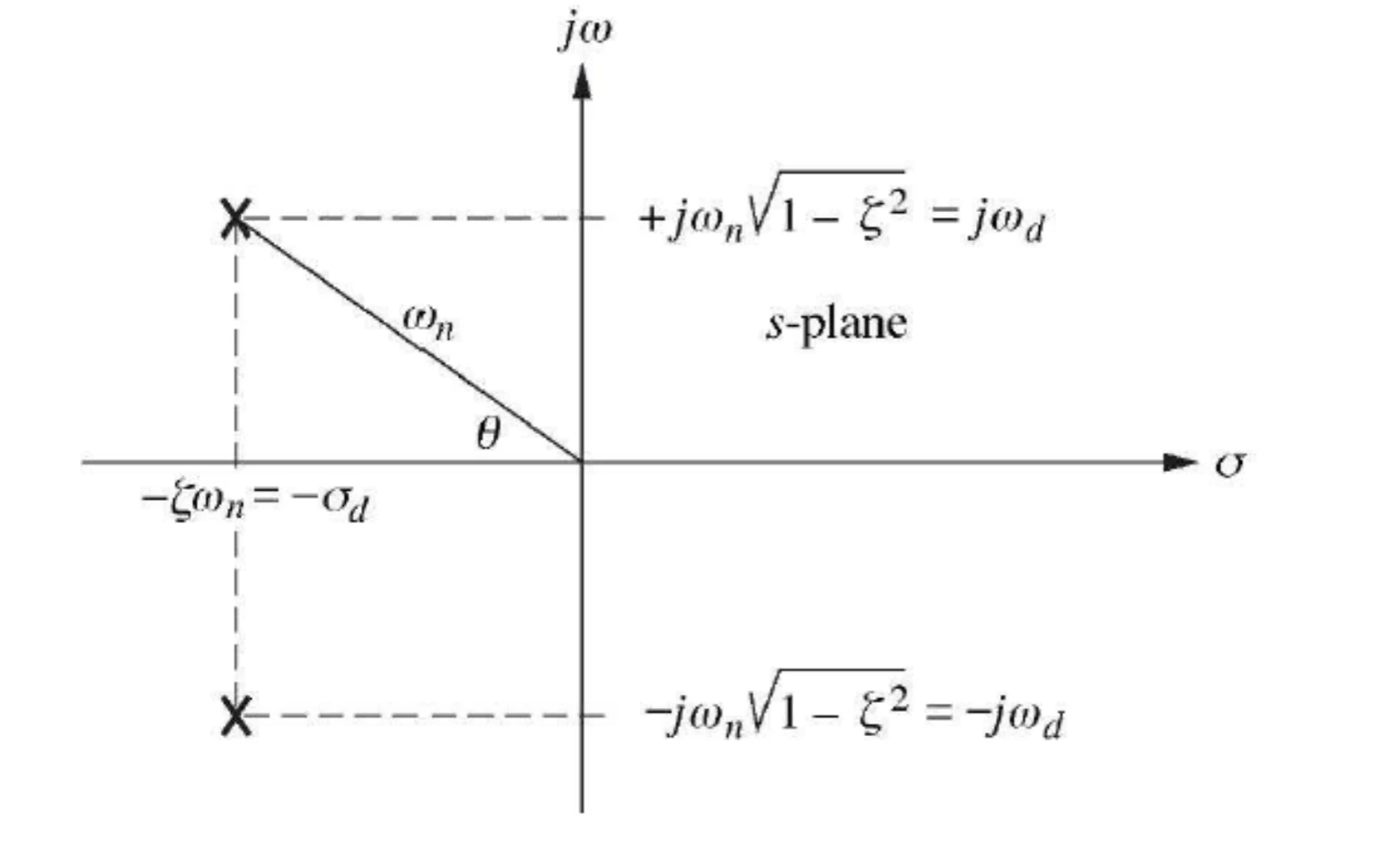
\end{aligned} G ( s ) s 1 , s 2 = s 2 + 2 ζ w n s + w n 2 w n 2 = − ζ w n ± w n ζ 2 − 1 observations Condition Poles pole type Damping Ratio (ζ \zeta ζ Natural Response c ( t ) c(t) c ( t ) Undamped ± j ω n \pm j \omega_n ± j ω n imaginary ζ = 0 \zeta = 0 ζ = 0 A cos ( ω n t − φ ) A \cos (\omega_n t - \varphi) A cos ( ω n t − φ ) Underdamped ω d ± j ω d \omega_d \pm j \omega_d ω d ± j ω d complex 0 < ζ < 1 0 < \zeta < 1 0 < ζ < 1 A e ( − σ d ) t cos ( ω d t − φ ) A e^{(-\sigma_d)t} \cos (\omega_d t - \varphi) A e ( − σ d ) t cos ( ω d t − φ ) w d = w n 1 − ζ 2 w_d = w_n \sqrt{1- \zeta^2} w d = w n 1 − ζ 2 critically damped σ 1 \sigma_1 σ 1 real ζ = 1 \zeta = 1 ζ = 1 K t e σ 1 t K t e^{\sigma_1 t} K t e σ 1 t overdamped σ 1 σ 2 \sigma_1 \quad \sigma_2 σ 1 σ 2 real ζ > 1 \zeta > 1 ζ > 1 K ( e σ 1 t + e σ 2 t ) K (e^{\sigma_1 t} + e^{\sigma_2 t}) K ( e σ 1 t + e σ 2 t )
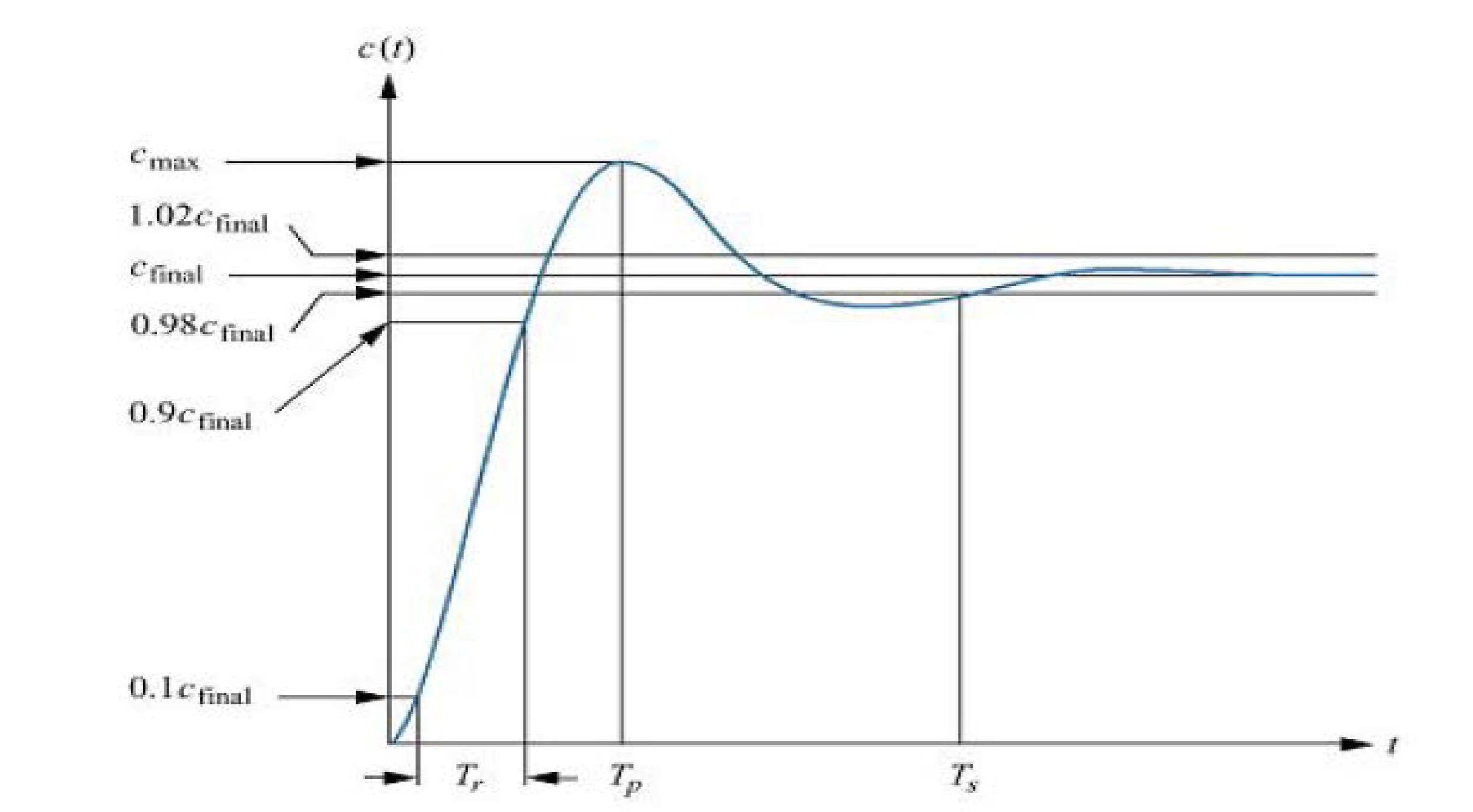
underdamped second-order step response Transfer function C ( s ) C(s) C ( s )
C ( s ) = w n 2 s ( s 2 + 2 ζ w n s + w n 2 ) C(s) = \frac{w_n^2}{s(s^2 + 2 \zeta w_n s + w_n^2)} C ( s ) = s ( s 2 + 2 ζ w n s + w n 2 ) w n 2 response in time-domain via inverse Laplace transform:
c ( t ) = 1 − 1 1 − ζ 2 e − ζ w n t cos ( 1 − ζ 2 ω n t + φ ) c(t) = 1 - \frac{1}{\sqrt{1- \zeta^2}} e^{- \zeta w_n t} \cos (\sqrt{1- \zeta^2}\omega_n t + \varphi) c ( t ) = 1 − 1 − ζ 2 1 e − ζ w n t cos ( 1 − ζ 2 ω n t + φ ) where φ = tan − 1 ( ζ 1 − ζ 2 ) \varphi = \tan^{-1} (\frac{\zeta}{\sqrt{1-\zeta^2}}) φ = tan − 1 ( 1 − ζ 2 ζ )
peak time T p T_p T p time required to reach the first or maximum peak
T p = π ω n 1 − ζ 2 T_p = \frac{\pi}{\omega_n \sqrt{1-\zeta^2}} T p = ω n 1 − ζ 2 π percent overshoot %OS (percent overshoot) % O S = e ζ π / 1 − ζ 2 × 100 % \%OS = e^{\zeta \pi / \sqrt{1-\zeta^2}} \times 100 \% % OS = e ζ π / 1 − ζ 2 × 100% or in terms of damping ratio ζ \zeta ζ
ζ = − ln %OS 100 π 2 + ln 2 ( %OS 100 ) \zeta = \frac{-\ln \frac{\text{\%OS}}{100}}{\sqrt{\pi^2 + \ln^2(\frac{\text{\%OS}}{100})}} ζ = π 2 + ln 2 ( 100 %OS ) − ln 100 %OS relations to poles G ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 s 1 , s 2 = − ζ w n ± w n ζ 2 − 1 T p = π ω n 1 − ζ 2 T s ≅ 4 ζ ω n \begin{aligned}
G(s) &= \frac{w_n^2}{s^2 + 2 \zeta w_n s + w_n^2} \\[12pt]
s_{1},s_{2} &= - \zeta w_n \pm w_n \sqrt{\zeta^2 - 1} \\[8pt]
T_p &= \frac{\pi}{\omega_n \sqrt{1-\zeta^2}} \\
T_s &\cong \frac{4}{\zeta \omega_n}
\end{aligned} G ( s ) s 1 , s 2 T p T s = s 2 + 2 ζ w n s + w n 2 w n 2 = − ζ w n ± w n ζ 2 − 1 = ω n 1 − ζ 2 π ≅ ζ ω n 4 figure 1 : poles of second-order underdamped system same envelope "\\usepackage{tikz}\n\\usepackage{pgfplots}\n\\pgfplotsset{compat=1.16}\n\n\\begin{document}\n\\begin{tikzpicture}\n \\begin{axis}[\n width=12cm, height=8cm,\n xlabel={$t$ (time)},\n ylabel={Amplitude},\n grid=major,\n legend style={at={(0.5,1.1)}, anchor=north, legend columns=-1},\n xmin=0, xmax=10,\n ymin=-1.2, ymax=1.2\n ]\n % First Transfer Function (Sinusoidal)\n \\addplot[blue, thick, samples=100, domain=0:10]\n {exp(-0.1*x)*sin(deg(2*pi*0.5*x))};\n\n % Second Transfer Function (Envelope with Different Frequency)\n \\addplot[red, dashed, thick, samples=100, domain=0:10]\n {exp(-0.1*x)*sin(deg(2*pi*0.8*x))};\n\n % Envelope (Exponential Decay)\n \\addplot[black, dotted, thick, samples=100, domain=0:10]\n {exp(-0.1*x)};\n\n \\addplot[black, dotted, thick, samples=100, domain=0:10]\n {-exp(-0.1*x)};\n \\end{axis}\n\\end{tikzpicture}\n\\end{document}" 0 1 2 3 4 5 6 7 8 9 10 ¡ 1 ¡ 0 : 5 0 0 : 5 1 t (time) Amplitude source code same frequency "\\usepackage{tikz}\n\\usepackage{pgfplots}\n\\pgfplotsset{compat=1.16}\n\n\\begin{document}\n\\begin{tikzpicture}\n \\begin{axis}[\n width=12cm, height=8cm,\n xlabel={$t$ (time)},\n ylabel={Amplitude},\n grid=major,\n legend style={at={(0.5,1.1)}, anchor=north, legend columns=-1},\n xmin=0, xmax=10,\n ymin=-3, ymax=3\n ]\n % First Transfer Function (Higher Amplitude)\n \\addplot[blue, thick, samples=100, domain=0:10]\n {2*sin(deg(2*pi*0.5*x))};\n\n % Second Transfer Function (Lower Amplitude)\n \\addplot[red, dashed, thick, samples=100, domain=0:10]\n {1*sin(deg(2*pi*0.5*x))};\n \\end{axis}\n\\end{tikzpicture}\n\\end{document}" 0 1 2 3 4 5 6 7 8 9 10 ¡ 3 ¡ 2 ¡ 1 0 1 2 3 t (time) Amplitude source code same overshoot "\\usepackage{tikz}\n\\usepackage{pgfplots}\n\\pgfplotsset{compat=1.16}\n\n\\begin{document}\n\\begin{tikzpicture}\n \\begin{axis}[\n width=12cm, height=8cm,\n xlabel={Time $t$},\n ylabel={Response},\n grid=major,\n legend style={at={(0.5,1.1)}, anchor=north, legend columns=-1},\n xmin=0, xmax=10,\n ymin=0, ymax=2\n ]\n % First System Response\n \\addplot[blue, thick, samples=200, domain=0:10]\n {1 - exp(-0.5*x)*(cos(deg(2*pi*0.5*x)) + 0.1*sin(deg(2*pi*0.5*x)))};\n\n % Second System Response (Same Overshoot, Different Natural Frequency)\n \\addplot[red, dashed, thick, samples=200, domain=0:10]\n {1 - exp(-1*x)*(cos(deg(2*pi*1*x)) + 0.05*sin(deg(2*pi*1*x)))};\n\n % Reference Line for Steady-State Response\n \\addplot[black, dotted, thick] coordinates {(0,1) (10,1)};\n \\end{axis}\n\\end{tikzpicture}\n\\end{document}" 0 1 2 3 4 5 6 7 8 9 10 0 0 : 5 1 1 : 5 2 Time t Resp onse source code reference:
excerpt from
If a system is stable and has a final constant value, then one can find steady state value without solving for system’s response. Formally:
lim t → ∞ x ( t ) = lim s → 0 s X ( s ) \lim_{t \to \infty} x(t) = \lim_{s \to 0} sX(s) t → ∞ lim x ( t ) = s → 0 lim s X ( s )
sketching root locus Rule Description Number of Branches Number of closed-loop poles , or the number of finite open-loop poles = number of finite open-loop zeros Symmetry About the real axis Start and End Points Starts at poles of open loop transfer function and ends at finite and infinite open loop zeros Behaviour at ∞ \infty ∞ Real axis: σ a = Σ finite poles − Σ finite zeros # finite poles - # finite zeros \sigma_a = \frac{\Sigma{\text{finite poles}} - \Sigma{\text{finite zeros}}}{\text{\# finite poles - \# finite zeros}} σ a = # finite poles - # finite zeros Σ finite poles − Σ finite zeros θ a = ( 2 k + 1 ) π # finite poles - # finite zeros \theta_a = \frac{(2k+1)\pi}{\text{\# finite poles - \# finite zeros}} θ a = # finite poles - # finite zeros ( 2 k + 1 ) π k = 0 , ± 1 , ± 2 , ± 3 k = 0, \pm 1, \pm 2, \pm 3 k = 0 , ± 1 , ± 2 , ± 3 Breakaway/Break-in Points Located at roots where d [ G ( s ) H ( s ) ] d s = 0 \frac{d[G(s)H(s)]}{ds} = 0 d s d [ G ( s ) H ( s )] = 0
Control Type Transfer function T ( s ) T(s) T ( s ) Key Characteristics Effects Proportional (P) K p G p 1 + K p G p \frac{K_p G_p}{1 + K_p G_p} 1 + K p G p K p G p Basic control action - Affects speed of response Integral (I) K I s 2 + s + K I \frac{K_I}{s^2 + s + K_I} s 2 + s + K I K I Integrates error over time - Eliminates steady-state error PI K I + s K p s 2 + ( 1 + K p ) s + K I \frac{K_I + sK_p}{s^2 + (1+K_p)s + K_I} s 2 + ( 1 + K p ) s + K I K I + s K p Combines P and I - P impacts response speed Derivative (D) K D s ( 1 + K D ) s + 1 \frac{K_D s}{(1+K_D)s + 1} ( 1 + K D ) s + 1 K D s Based on rate of change - Adds open-loop zero
PID control G C ( s ) = K p + K I s + K D s G_C(s) = K_p + \frac{K_I}{s} + K_D s G C ( s ) = K p + s K I + K D s in time domain:
u ( t ) = K P e ( t ) + K I ∫ 0 t e ( η ) d η + K D d ( e ( t ) ) d t u(t) = K_P e(t) + K_I \int_{0}^{t} e(\eta) d\eta + K_D \frac{d(e(t))}{dt} u ( t ) = K P e ( t ) + K I ∫ 0 t e ( η ) d η + K D d t d ( e ( t )) Component Discrete-Time Equation Proportional u ( k ) = K P e ( k ) u(k) = K_P e(k) u ( k ) = K P e ( k ) Integral u ( k ) = K I T ∑ i = 1 k e ( i ) u(k) = K_I T \sum_{i=1}^{k} e(i) u ( k ) = K I T ∑ i = 1 k e ( i ) Derivative u ( k ) = K D T [ e ( k ) − e ( k − 1 ) ] u(k) = \frac{K_D}{T}[e(k) - e(k-1)] u ( k ) = T K D [ e ( k ) − e ( k − 1 )]
approximate of PID controller: u ( k ) = K P e ( k ) + K I T ∑ i = 1 n e ( i ) + K D T [ e ( k ) − e ( k − 1 ) ] u(k) = K_P e(k) + K_I T \sum_{i=1}^{n} e(i) + \frac{K_D}{T}[e(k) - e(k-1)] u ( k ) = K P e ( k ) + K I T ∑ i = 1 n e ( i ) + T K D [ e ( k ) − e ( k − 1 )]
Time Domain x ( t ) x(t) x ( t ) Laplace Transform X ( s ) X(s) X ( s ) Z Transform X ( z ) X(z) X ( z ) δ ( t ) = { 1 t = 0 0 t = k T , k ≠ 0 \delta(t) = \begin{cases} 1 & t = 0 \\ 0 & t = kT, k \neq 0 \end{cases} δ ( t ) = { 1 0 t = 0 t = k T , k = 0 1 1 1 1 1 1 δ ( t − k T ) = { 1 t = k T 0 t ≠ k T \delta(t - kT) = \begin{cases} 1 & t = kT \\ 0 & t \neq kT \end{cases} δ ( t − k T ) = { 1 0 t = k T t = k T e − k T s e^{-kTs} e − k T s z − k z^{-k} z − k u ( t ) u(t) u ( t ) 1 s \frac{1}{s} s 1 z z − 1 \frac{z}{z - 1} z − 1 z t t t 1 s 2 \frac{1}{s^2} s 2 1 T z ( z − 1 ) 2 \frac{Tz}{(z - 1)^2} ( z − 1 ) 2 T z t 2 t^2 t 2 2 s 3 \frac{2}{s^3} s 3 2 T 2 z ( z + 1 ) ( z − 1 ) 3 \frac{T^2 z(z + 1)}{(z - 1)^3} ( z − 1 ) 3 T 2 z ( z + 1 ) e − a t e^{-at} e − a t 1 s + a \frac{1}{s + a} s + a 1 z z − e − a T \frac{z}{z - e^{-aT}} z − e − a T z 1 − e − a t 1 - e^{-at} 1 − e − a t a s ( s + a ) \frac{a}{s(s + a)} s ( s + a ) a ( 1 − e − a T ) z ( z − 1 ) ( z − e − a T ) \frac{(1 - e^{-aT})z}{(z - 1)(z - e^{-aT})} ( z − 1 ) ( z − e − a T ) ( 1 − e − a T ) z t e − a t te^{-at} t e − a t 1 ( s + a ) 2 \frac{1}{(s + a)^2} ( s + a ) 2 1 T z e − a T ( z − e − a T ) 2 \frac{Tz e^{-aT}}{(z - e^{-aT})^2} ( z − e − a T ) 2 T z e − a T t 2 e − a t t^2 e^{-at} t 2 e − a t 2 ( s + a ) 3 \frac{2}{(s + a)^3} ( s + a ) 3 2 T 2 e − a T z ( z + e − a T ) ( z − e − a T ) 3 \frac{T^2 e^{-aT} z(z + e^{-aT})}{(z - e^{-aT})^3} ( z − e − a T ) 3 T 2 e − a T z ( z + e − a T ) b e − b t − a e − a t b e^{-bt} - a e^{-at} b e − b t − a e − a t ( b − a ) s ( s + a ) ( s + b ) \frac{(b - a)s}{(s + a)(s + b)} ( s + a ) ( s + b ) ( b − a ) s z [ z ( b − a ) − ( b e − a T − a e − b T ) ] ( z − e − a T ) ( z − e − b T ) \frac{z [ z(b - a) - (b e^{-aT} - a e^{-bT}) ]}{(z - e^{-aT})(z - e^{-bT})} ( z − e − a T ) ( z − e − b T ) z [ z ( b − a ) − ( b e − a T − a e − b T )] sin ω t \sin \omega t sin ω t ω s 2 + ω 2 \frac{\omega}{s^2 + \omega^2} s 2 + ω 2 ω z sin ω T z 2 − 2 z cos ω T + 1 \frac{z \sin \omega T}{z^2 - 2z \cos \omega T + 1} z 2 − 2 z c o s ω T + 1 z s i n ω T cos ω t \cos \omega t cos ω t s s 2 + ω 2 \frac{s}{s^2 + \omega^2} s 2 + ω 2 s z ( z − cos ω T ) z 2 − 2 z cos ω T + 1 \frac{z(z - \cos \omega T)}{z^2 - 2z \cos \omega T + 1} z 2 − 2 z c o s ω T + 1 z ( z − c o s ω T ) e − a t sin ω t e^{-at} \sin \omega t e − a t sin ω t ω ( s + a ) 2 + ω 2 \frac{\omega}{(s + a)^2 + \omega^2} ( s + a ) 2 + ω 2 ω z e − a T sin ω T z 2 − 2 z e − a T cos ω T + e − 2 a T \frac{z e^{-aT} \sin \omega T}{z^2 - 2z e^{-aT} \cos \omega T + e^{-2aT}} z 2 − 2 z e − a T c o s ω T + e − 2 a T z e − a T s i n ω T
reference:
Sequence Transform δ ( k − n ) \delta(k - n) δ ( k − n ) z − n z^{-n} z − n 1 1 1 z z − 1 \frac{z}{z - 1} z − 1 z k k k z ( z − 1 ) 2 \frac{z}{(z - 1)^2} ( z − 1 ) 2 z k 2 k^2 k 2 z ( z + 1 ) ( z − 1 ) 3 \frac{z(z + 1)}{(z - 1)^3} ( z − 1 ) 3 z ( z + 1 ) a k a^k a k z z − a \frac{z}{z - a} z − a z k a k ka^k k a k a z ( z − a ) 2 \frac{az}{(z - a)^2} ( z − a ) 2 a z sin a k \sin ak sin ak z sin a z 2 − 2 z cos a + 1 \frac{z \sin a}{z^2 - 2z \cos a + 1} z 2 − 2 z c o s a + 1 z s i n a cos a k \cos ak cos ak z ( z − cos a ) z 2 − 2 z cos a + 1 \frac{z(z - \cos a)}{z^2 - 2z \cos a + 1} z 2 − 2 z c o s a + 1 z ( z − c o s a ) a k sin b k a^k \sin bk a k sin bk a z sin b z 2 − 2 a z cos b + a 2 \frac{az \sin b}{z^2 - 2az \cos b + a^2} z 2 − 2 a z c o s b + a 2 a z s i n b a k cos b k a^k \cos bk a k cos bk z 2 − a z cos b z 2 − 2 a z cos b + a 2 \frac{z^2 - az \cos b}{z^2 - 2az \cos b + a^2} z 2 − 2 a z c o s b + a 2 z 2 − a z c o s b
properties Linearity : if x ( n ) = a f 1 ( n ) + b f 2 ( n ) x(n) = af_{1}(n) + bf_{2}(n) x ( n ) = a f 1 ( n ) + b f 2 ( n ) X ( z ) = a F 1 ( z ) + b F 2 ( z ) X(z) = aF_{1}(z) + bF_{2}(z) X ( z ) = a F 1 ( z ) + b F 2 ( z )
Time shifting :
Z [ x ( t ) ] = X ( z ) x ( k − n ) = z − n X ( z ) x ( k + n ) = z n X ( z ) \begin{aligned}
Z[x(t)] &= X(z) \\
x(k-n) &= z^{-n}X(z) \\
x(k+n) &= z^{n}X(z)
\end{aligned} Z [ x ( t )] x ( k − n ) x ( k + n ) = X ( z ) = z − n X ( z ) = z n X ( z )
The idea to convert analog to digital
T T T 1 T \frac{1}{T} T 1 cycles per second
error = M 2 n + 1 \text{error} = \frac{M}{2^{n+1}} error = 2 n + 1 M where n n n
resolution of A/D converter
minimum value of the output that can be represented as binary number, or M 2 n \frac{M}{2^n} 2 n M
sampled data system reference input r r r r ( k T ) r(kT) r ( k T )
A sampler is a switch that closes every T T T
r ∗ ( t ) = ∑ k = 0 ∞ r ( k T ) δ ( t − k T ) ( t > 0 ) r^{*}(t) = \sum_{k=0}^{\infty} r(kT) \delta (t-kT) \quad (t>0) r ∗ ( t ) = k = 0 ∑ ∞ r ( k T ) δ ( t − k T ) ( t > 0 ) Transfer function of sampled data:
R ∗ ( s ) = L ( r ∗ ( t ) ) = ∑ k = 0 ∞ r ( k T ) e − k s T R^{*}(s) = \mathcal{L} (r^{*}(t)) = \sum_{k=0}^{\infty} r(kT) e^{-ksT} R ∗ ( s ) = L ( r ∗ ( t )) = k = 0 ∑ ∞ r ( k T ) e − k s T definition Let z = e s T z = e^{sT} z = e s T
Z { r ( t ) } = F ( z ) = Z ( r ∗ ( t ) ) = ∑ k = 0 ∞ r ( k T ) z − k Z \{r(t)\} = F(z) = Z(r^{*}(t)) = \sum_{k=0}^{\infty} r(kT)z^{-k} Z { r ( t )} = F ( z ) = Z ( r ∗ ( t )) = k = 0 ∑ ∞ r ( k T ) z − k
zero-order hold Transfer function of Zero-Order hold
L ( u ( t ) − u ( t − T ) ) = 1 s − e s T s \mathcal{L}(u(t) - u(t-T)) = \frac{1}{s} - \frac{e^{sT}}{s} L ( u ( t ) − u ( t − T )) = s 1 − s e s T finding the discrete transfer function G ( s ) = s 2 + 4 s + 3 s 3 + 6 s 2 + 8 s G(s) = \frac{s^2 + 4s + 3}{s^3 + 6s^2 + 8s} G ( s ) = s 3 + 6 s 2 + 8 s s 2 + 4 s + 3
G ( s ) = s 2 + 4 s + 3 s 3 + 6 s 2 + 8 s = 0.375 s + 0.25 s + 2 + 0.375 s + 4 G ( t ) = L − 1 ( G ( s ) ) = 0.375 + 0.25 e − 2 t + 0.375 e − 4 t G ( z ) = Z ( G ( t ) ) = 0.375 z z − 1 + 0.25 z z − e − 2 T + 0.375 z z − e − 4 T \begin{aligned}
G(s) &= \frac{s^2 + 4s + 3}{s^3 + 6s^2 + 8s} = \frac{0.375}{s} + \frac{0.25}{s+2} + \frac{0.375}{s+4} \\
G(t) &= \mathcal{L}^{-1}(G(s)) = 0.375 + 0.25 e^{-2t} + 0.375 e^{-4t} \\
G(z) &= Z(G(t)) = 0.375 \frac{z}{z-1} + 0.25 \frac{z}{z-e^{-2T}} + 0.375 \frac{z}{z-e^{-4T}}
\end{aligned} G ( s ) G ( t ) G ( z ) = s 3 + 6 s 2 + 8 s s 2 + 4 s + 3 = s 0.375 + s + 2 0.25 + s + 4 0.375 = L − 1 ( G ( s )) = 0.375 + 0.25 e − 2 t + 0.375 e − 4 t = Z ( G ( t )) = 0.375 z − 1 z + 0.25 z − e − 2 T z + 0.375 z − e − 4 T z G ( z ) → x ( k ) G(z) \to x(k) G ( z ) → x ( k )
power series use: when G(z) is expressed as the ratio of two polynomials in z
G ( z ) = a 0 + a 1 z − 1 + a 2 z − 2 + … G(z) = a_{0} + a_{1} z^{-1} + a_{2} z^{-2} + \ldots G ( z ) = a 0 + a 1 z − 1 + a 2 z − 2 + … partial fraction For example: G ( z ) = z ( z − 1 ) ( z − 2 ) = − z z − 1 + z z − 2 = ∑ k = 0 ∞ ( − 1 + 2 k ) z − k G(z) = \frac{z}{(z-1)(z-2)} = \frac{-z}{z-1} + \frac{z}{z-2} = \sum_{k=0}^{\infty} (-1 + 2^k)z^{-k} G ( z ) = ( z − 1 ) ( z − 2 ) z = z − 1 − z + z − 2 z = ∑ k = 0 ∞ ( − 1 + 2 k ) z − k
thus, g ( k T ) = 2 k − 1 g(kT) = 2^k-1 g ( k T ) = 2 k − 1
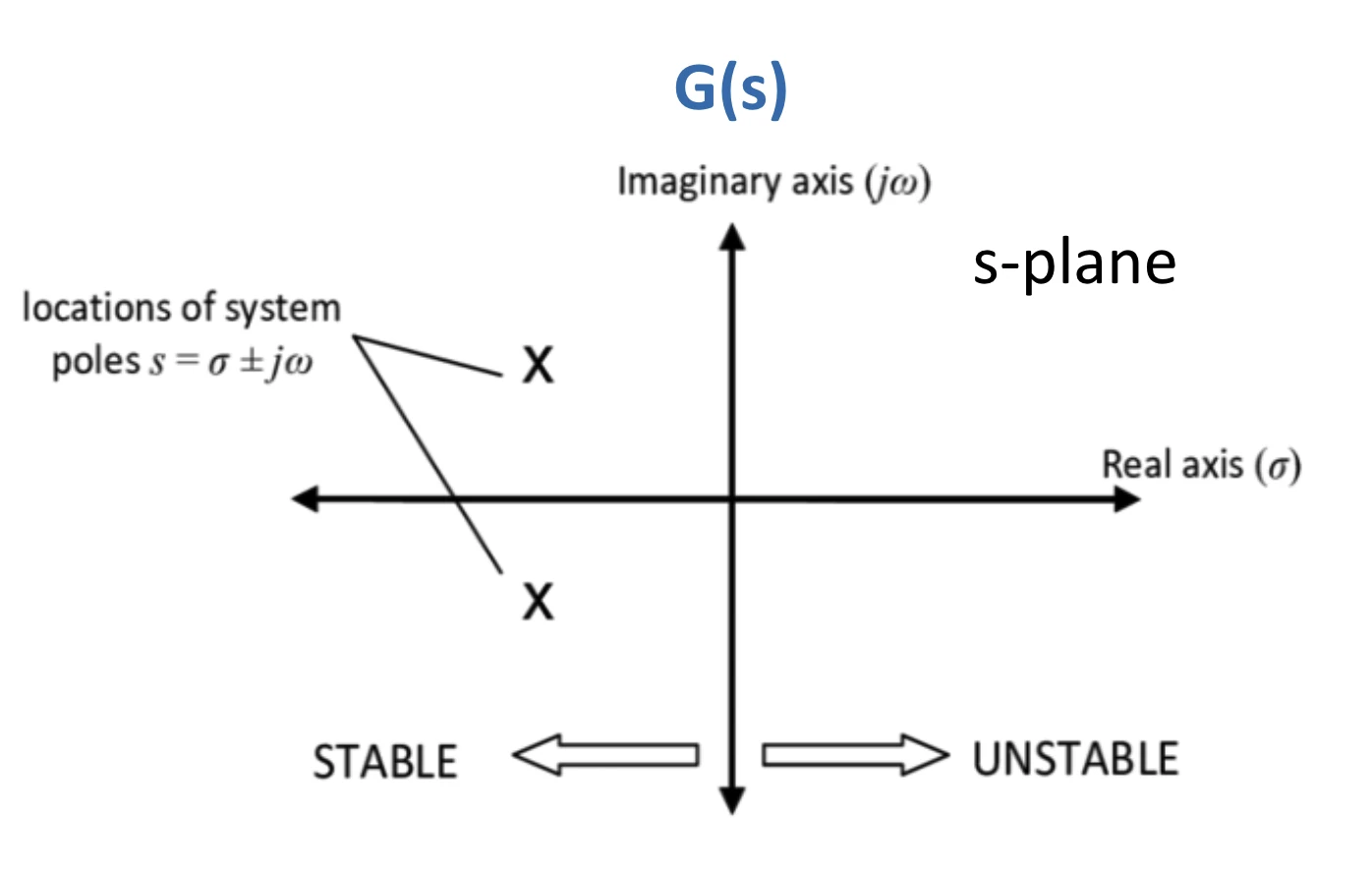
stability system pole location criteria on z-plane Stable All poles inside unit circle Unstable Any poles outside unit circle Marginally Stable One or more poles on unit circle, remaining poles inside unit circle
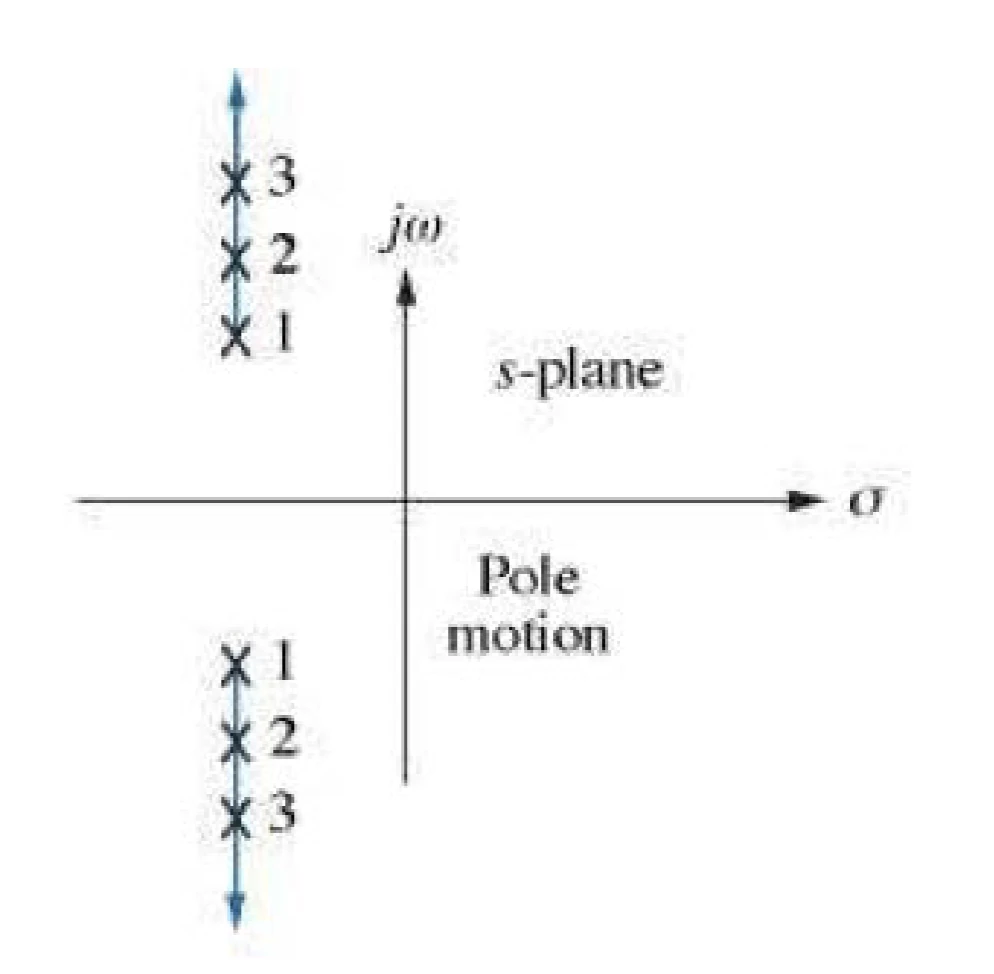
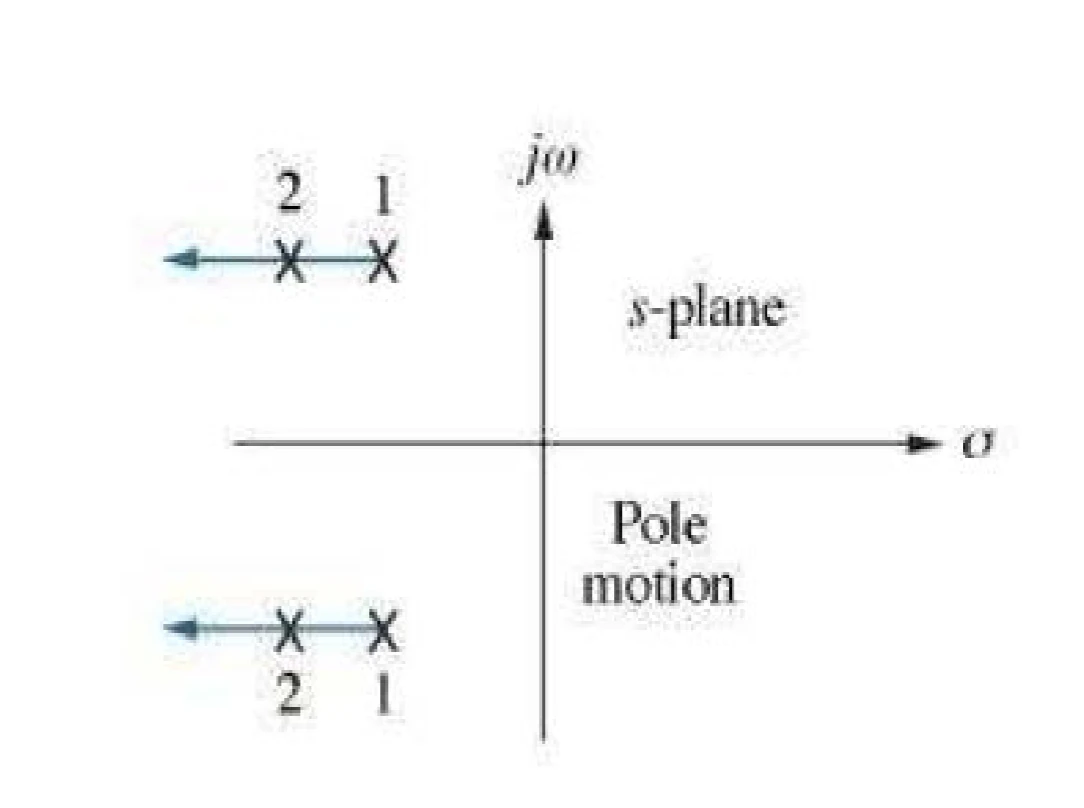
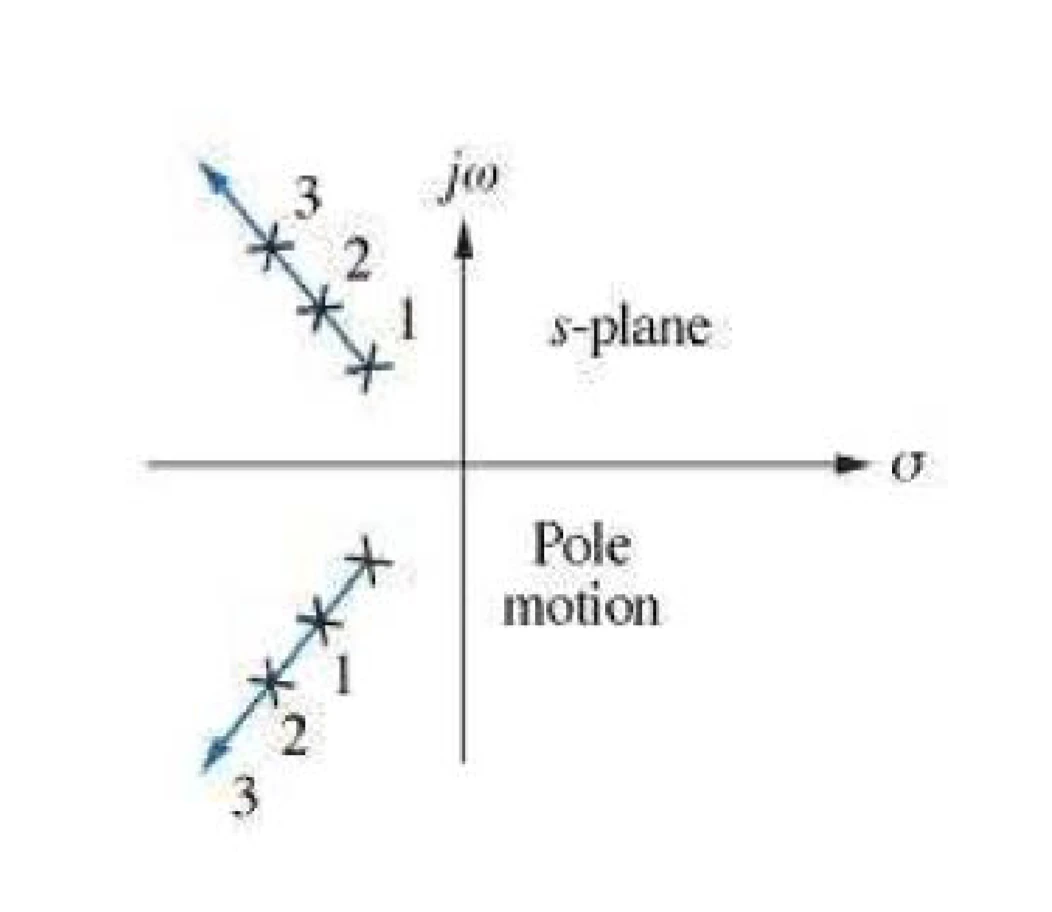
figure 1 : poles on s-plane
mapping from s-plane to z-plane
z = e α T ( cos ω T + j sin ω T ) z = e^{\alpha T}(\cos \omega T + j \sin \omega T) z = e α T ( cos ω T + j sin ω T )
we assume s = α + j ω s = \alpha + j \omega s = α + jω Location on s-plane Value of α \alpha α Value of e α T e^{\alpha T} e α T Mapping on z-plane Imaginary axis (j ω j\omega jω α = 0 \alpha = 0 α = 0 e α T = 1 e^{\alpha T} = 1 e α T = 1 On unit circle Right half-plane α > 0 \alpha > 0 α > 0 e α T > 1 e^{\alpha T} > 1 e α T > 1 Outside unit circle Left half-plane α < 0 \alpha < 0 α < 0 e α T < 1 e^{\alpha T} < 1 e α T < 1 Inside unit circle
final value theorem
If lim k → ∞ x ( k ) \lim_{k \to \infty}x(k) lim k → ∞ x ( k )
lim k → ∞ x ( k ) = lim z → 1 ( z − 1 ) X ( z ) \lim_{k \to \infty} x(k) = \lim_{z \to 1} (z-1) X(z) k → ∞ lim x ( k ) = z → 1 lim ( z − 1 ) X ( z )
derive open loop function K G H ˉ K \bar{GH} K G H ˉ
Factor numerator and denominator to get open loop zeros and poles
Plot roots of 1 + K G H ˉ = 0 1+K \bar{GH}=0 1 + K G H ˉ = 0 G H ( z ) ˉ = N ( z ) D ( z ) \bar{GH(z)} = \frac{N(z)}{D(z)} G H ( z ) ˉ = D ( z ) N ( z )
For determine discrete systems and vice versa.
G ( z ) G(z) G ( z ) G ( z ) = ( 1 − z − 1 ) Z [ G p ( s ) s ] = G ∗ ( z ) − z − 1 G ∗ ( z ) G(z) = (1-z^{-1}) Z[\frac{G_p(s)}{s}] = G^{*}(z) - z^{-1}G^{*}(z) G ( z ) = ( 1 − z − 1 ) Z [ s G p ( s ) ] = G ∗ ( z ) − z − 1 G ∗ ( z ) example: Find G ( z ) G(z) G ( z ) G p ( s ) = s + 2 s + 1 G_p(s) = \frac{s+2}{s+1} G p ( s ) = s + 1 s + 2
G ∗ ( s ) = G p ( s ) s = 2 s − 1 s + 1 g ∗ ( t ) = 2 − e − t ( inverse Laplace transform ) g ∗ ( k T ) = 2 − e − k T G ∗ ( z ) = 2 z z − 1 − z z − e − T \begin{aligned}
G^{*}(s) &= \frac{G_p(s)}{s} = \frac{2}{s} - \frac{1}{s+1} \\[8pt]
g^{*}(t) &= 2 - e^{-t} \quad (\text{inverse Laplace transform}) \\
g^{*}(kT) &= 2 - e^{-kT} \\
G^{*}(z) = \frac{2z}{z-1} - \frac{z}{z-e^{-T}}
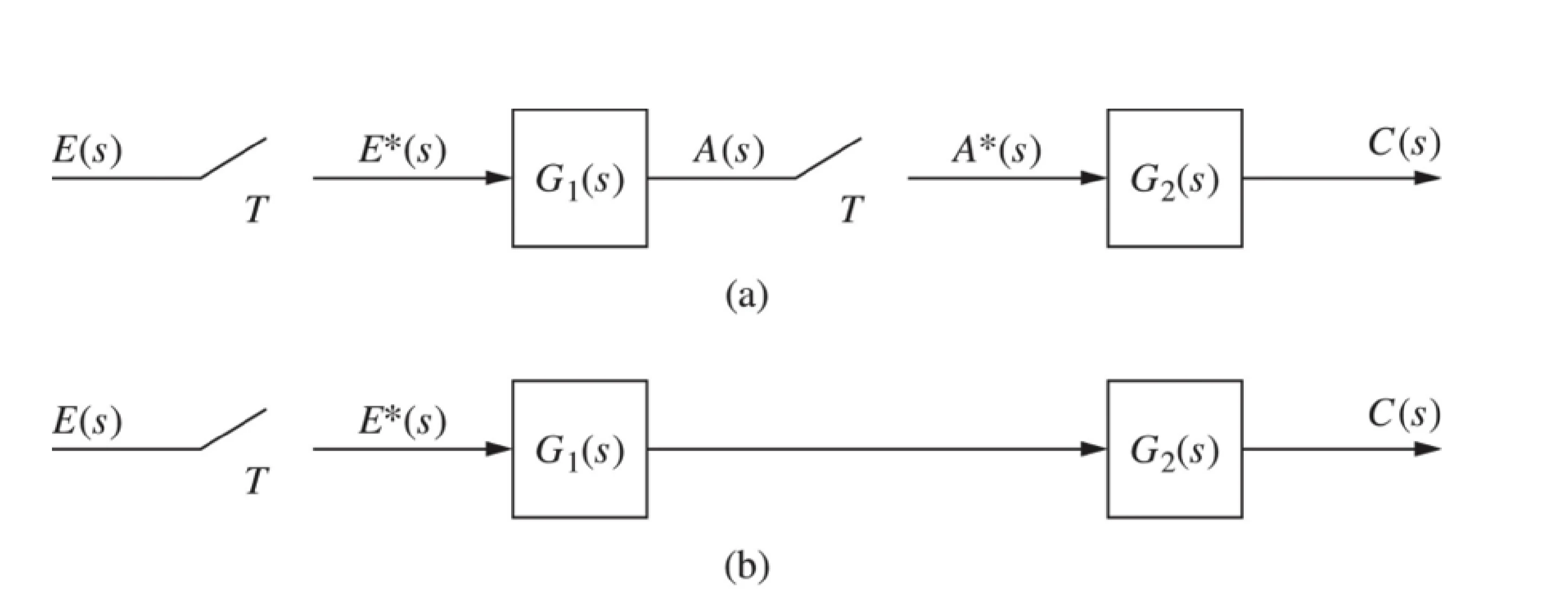
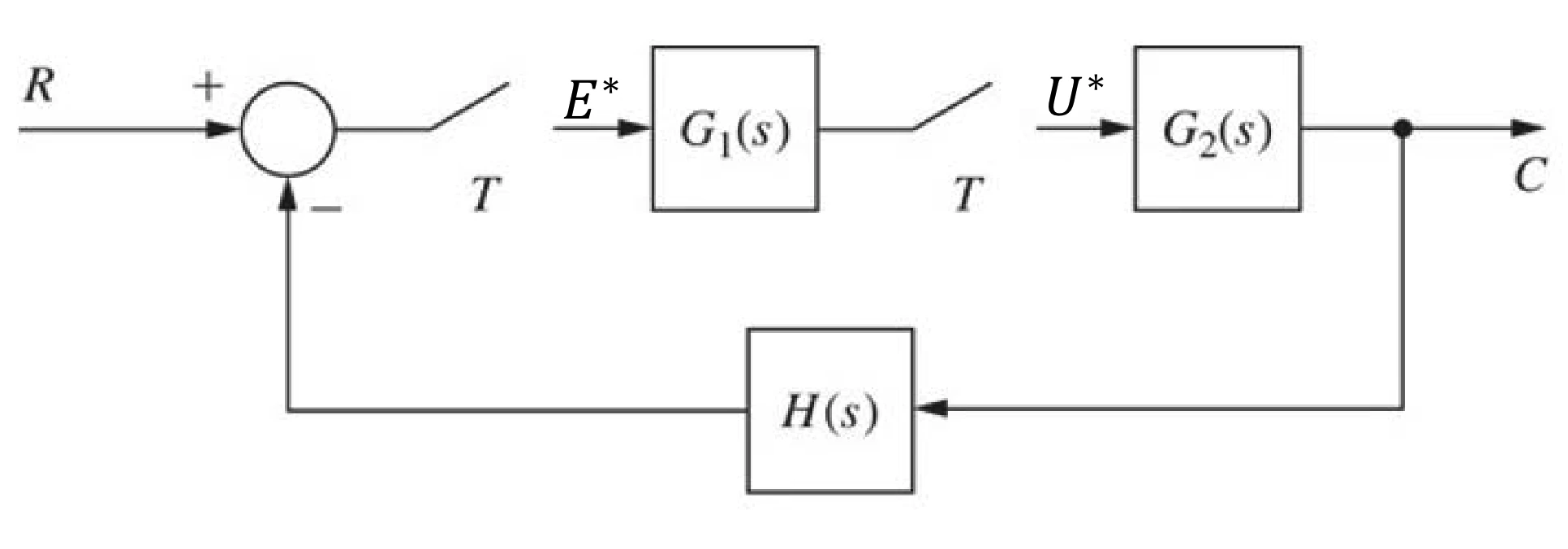
\end{aligned} G ∗ ( s ) g ∗ ( t ) g ∗ ( k T ) G ∗ ( z ) = z − 1 2 z − z − e − T z = s G p ( s ) = s 2 − s + 1 1 = 2 − e − t ( inverse Laplace transform ) = 2 − e − k T block diagram reduction a. C ( z ) = G 1 ( z ) G 2 ( z ) E ( z ) C(z) = G_1(z) G_2(z) E(z) C ( z ) = G 1 ( z ) G 2 ( z ) E ( z ) C ( z ) = Z [ G 1 ( s ) G 2 ( s ) ] E ( z ) C(z) = Z[G_1(s) G_2(s)]E(z) C ( z ) = Z [ G 1 ( s ) G 2 ( s )] E ( z )
The product of G 1 ( s ) G 2 ( s ) G_1(s)G_2(s) G 1 ( s ) G 2 ( s )
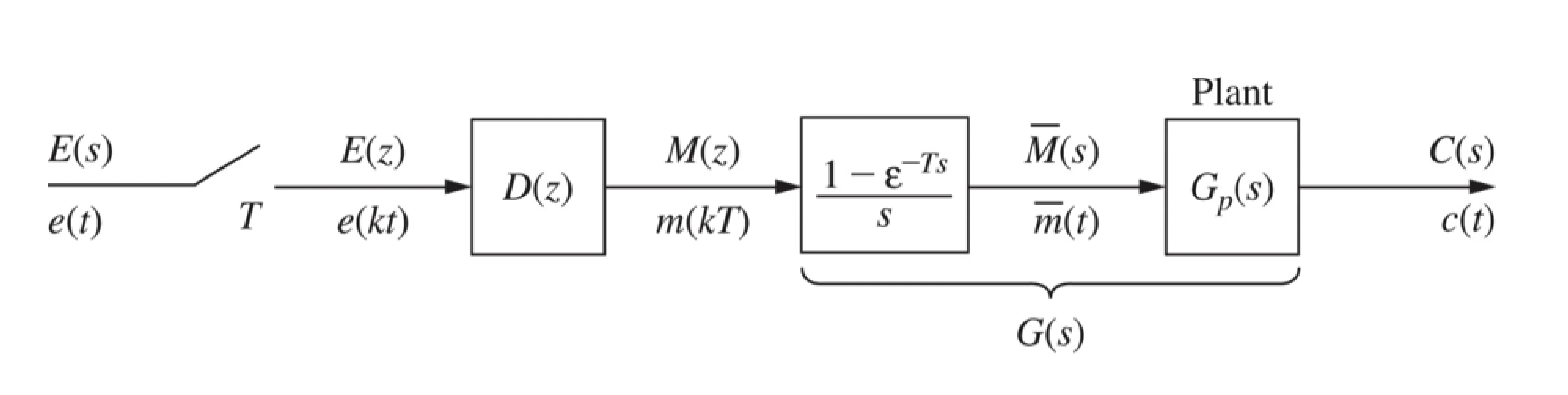
model for Open-loop system The output of open-loop system is
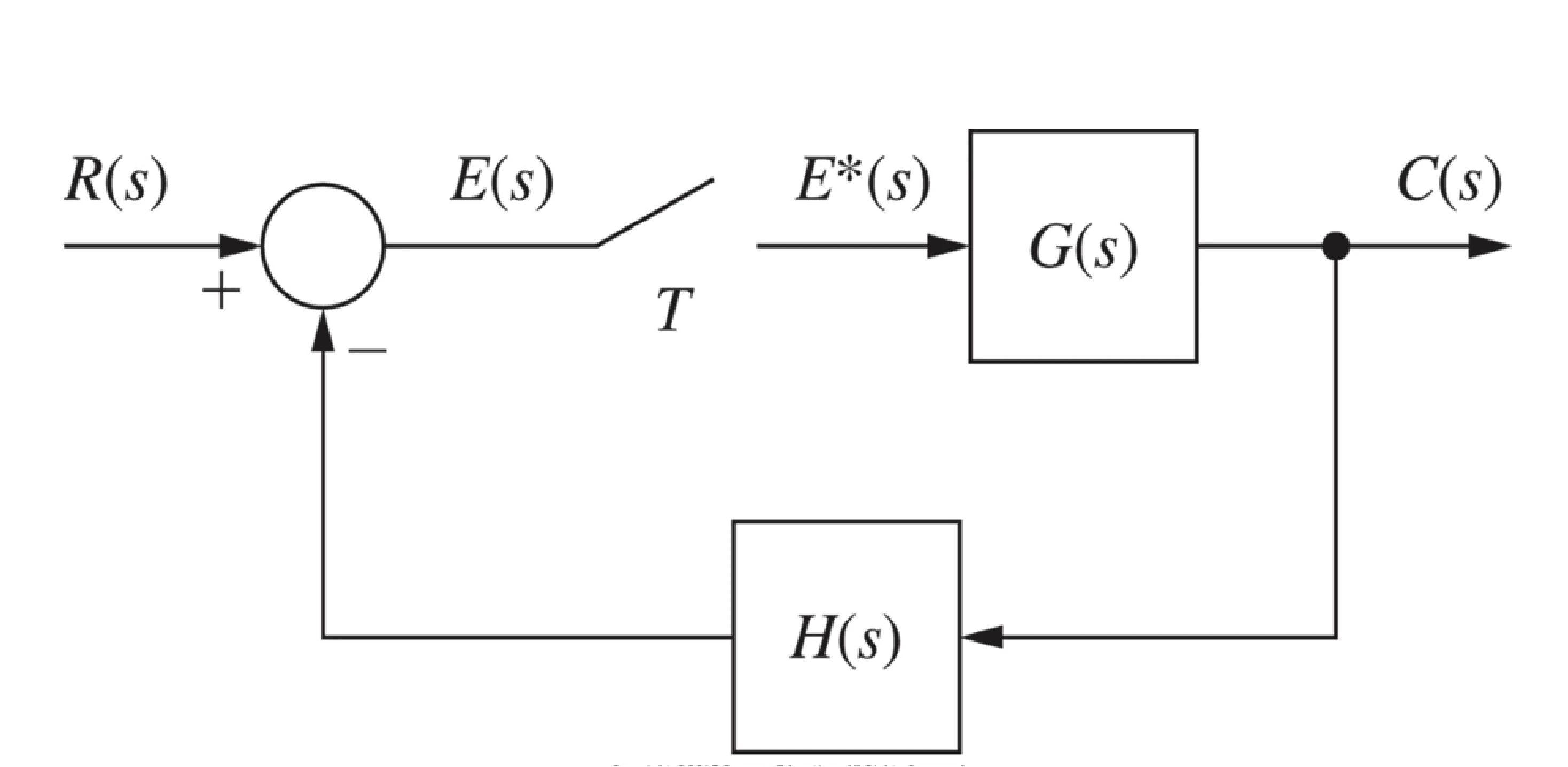
C ( z ) = G ( z ) D ( z ) E ( z ) C(z) = G(z)D(z)E(z) C ( z ) = G ( z ) D ( z ) E ( z ) closed loop sample data system E ( z ) = R ( z ) − Z [ G ( s ) H ( s ) ] E ( z ) ∵ C ( z ) R ( z ) = G ( z ) 1 + Z [ G ( s ) H ( s ) ] \begin{aligned}
E(z) &= R(z) - Z[G(s)H(s)]E(z) \\[12pt]
&\because \frac{C(z)}{R(z)} = \frac{G(z)}{1+Z[G(s)H(s)]}
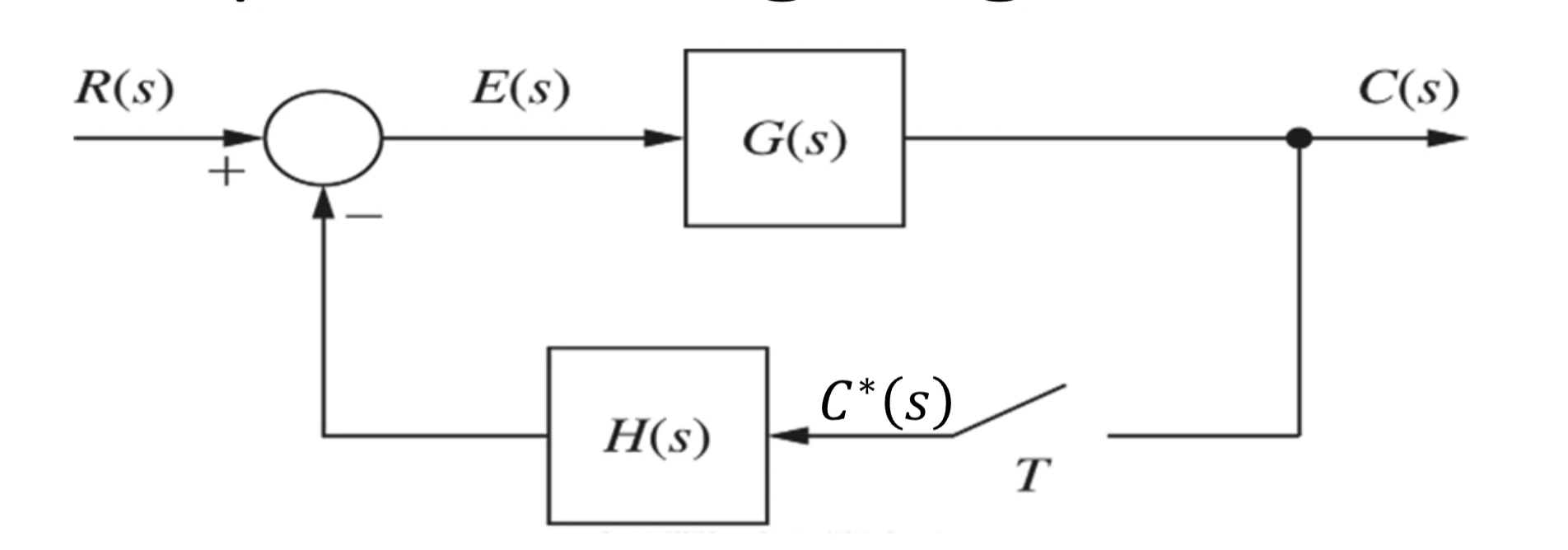
\end{aligned} E ( z ) = R ( z ) − Z [ G ( s ) H ( s )] E ( z ) ∵ R ( z ) C ( z ) = 1 + Z [ G ( s ) H ( s )] G ( z ) using digital sensing device C ( z ) = Z [ G ( s ) R ( s ) ] 1 + Z ( G ( s ) H ( s ) ) C(z) = \frac{Z[G(s)R(s)]}{1+Z(G(s)H(s))} C ( z ) = 1 + Z ( G ( s ) H ( s )) Z [ G ( s ) R ( s )] using digital controller C ( z ) R ( z ) = G 1 ( z ) G 1 ( z ) 1 + G 1 ( z ) Z ( G 2 ( s ) H ( s ) ) \frac{C(z)}{R(z)} = \frac{G_{1}(z)G_{1}(z)}{1+G_{1}(z)Z(G_{2}(s)H(s))} R ( z ) C ( z ) = 1 + G 1 ( z ) Z ( G 2 ( s ) H ( s )) G 1 ( z ) G 1 ( z ) time response T ( z ) = G ( z ) 1 + G ( z ) T(z) = \frac{G(z)}{1+G(z)} T ( z ) = 1 + G ( z ) G ( z ) System Type Transfer Function Diagram Basis C ( z ) R ( z ) = G ( z ) 1 + Z [ G ( s ) H ( s ) ] \frac{C(z)}{R(z)} = \frac{G(z)}{1+Z[G(s)H(s)]} R ( z ) C ( z ) = 1 + Z [ G ( s ) H ( s )] G ( z ) w/ digital sensing device C ( z ) = Z [ G ( s ) R ( s ) ] 1 + Z ( G ( s ) H ( s ) ) C(z) = \frac{Z[G(s)R(s)]}{1+Z(G(s)H(s))} C ( z ) = 1 + Z ( G ( s ) H ( s )) Z [ G ( s ) R ( s )] w/ digital controller C ( z ) R ( z ) = G 1 ( z ) G 1 ( z ) 1 + G 1 ( z ) Z ( G 2 ( s ) H ( s ) ) \frac{C(z)}{R(z)} = \frac{G_{1}(z)G_{1}(z)}{1+G_{1}(z)Z(G_{2}(s)H(s))} R ( z ) C ( z ) = 1 + G 1 ( z ) Z ( G 2 ( s ) H ( s )) G 1 ( z ) G 1 ( z )
Assume the transfer function is given by
D ( s ) = U ( s ) E ( s ) = K 0 s + a s + b D(s) = \frac{U(s)}{E(s)} = K_{0} \frac{s+a}{s+b} D ( s ) = E ( s ) U ( s ) = K 0 s + b s + a
u ( k ) = ( 1 − b T ) u ( k − 1 ) + K 0 ( a T − 1 ) E ( k − 1 ) + K 0 e ( k ) u(k) = (1-bT)u(k-1) + K_{0}(aT-1)E(k-1) + K_{0}e(k) u ( k ) = ( 1 − b T ) u ( k − 1 ) + K 0 ( a T − 1 ) E ( k − 1 ) + K 0 e ( k )
The corresponding z-transform
U ( z ) E ( z ) = K 0 ( a T − 1 ) z − 1 + K 0 1 + ( b T − 1 ) z − 1 = K 0 z + K 0 ( a T − 1 ) z + ( b T − 1 ) = [ K 0 ( a T − 1 ) + z K 0 ] / [ z + ( b T − 1 ) ] \begin{aligned}
\frac{U(z)}{E(z)} &= \frac{K_{0}(aT-1)z^{-1} + K_{0}}{1+(bT-1)z^{-1}} = \frac{K_{0}z + K_{0}(aT-1)}{z+(bT-1)} \\
&=[K_{0}(aT-1) + zK_{0}]/[z+(bT-1)]
\end{aligned} E ( z ) U ( z ) = 1 + ( b T − 1 ) z − 1 K 0 ( a T − 1 ) z − 1 + K 0 = z + ( b T − 1 ) K 0 z + K 0 ( a T − 1 ) = [ K 0 ( a T − 1 ) + z K 0 ] / [ z + ( b T − 1 )] example: Given D ( s ) = a s + a D(s) = \frac{a}{s+a} D ( s ) = s + a a u ( k T ) = u ( k ) u(kT) = u(k) u ( k T ) = u ( k )
U ( s ) ( s + a ) = a E ( s ) U(s)(s+a) = aE(s) U ( s ) ( s + a ) = a E ( s ) u ( k + 1 ) − u ( k ) T + a u ( k ) = a e ( k ) \frac{u(k+1)-u(k)}{T} + au(k) = a e(k) T u ( k + 1 ) − u ( k ) + a u ( k ) = a e ( k )
difference equation is u ( k + 1 ) = ( 1 − a T ) u ( k ) + a T e ( k ) u(k+1) = (1-aT)u(k) + aTe(k) u ( k + 1 ) = ( 1 − a T ) u ( k ) + a T e ( k )
z-transform is U ( z ) E ( z ) = a T z − 1 1 + ( a T − 1 ) z − 1 = a T z + ( a T − 1 ) \frac{U(z)}{E(z)}=\frac{aT z^{-1}}{1+(aT -1)z^{-1}}=\frac{aT}{z+(aT-1)} E ( z ) U ( z ) = 1 + ( a T − 1 ) z − 1 a T z − 1 = z + ( a T − 1 ) a T
discrete equivalent Consider the example
D ( s ) = U ( s ) E ( s ) = a s + a → U ( s ) s = a E ( s ) − a U ( s ) → u ′ ( t ) = − a u ( t ) + a e ( t ) \begin{aligned}
D(s) &= \frac{U(s)}{E(s)} = \frac{a}{s+a} \to U(s)s = aE(s) - aU(s) \\
&\to u^{'}(t) = -au(t) + ae(t)
\end{aligned} D ( s ) = E ( s ) U ( s ) = s + a a → U ( s ) s = a E ( s ) − a U ( s ) → u ′ ( t ) = − a u ( t ) + a e ( t ) u ( t ) = ∫ 0 t [ − a u ( τ ) + a e ( τ ) ] d τ u(t) = \int_0^t [-au(\tau) + ae(\tau)] d \tau u ( t ) = ∫ 0 t [ − a u ( τ ) + a e ( τ )] d τ
u ( k T ) = u ( k T − T ) + ∫ k T − T k T [ − a u ( τ ) + a e ( τ ) ] d τ u(kT) = u(kT - T) + \int_{kT-T}^{kT} [-au(\tau) + ae(\tau)] d \tau u ( k T ) = u ( k T − T ) + ∫ k T − T k T [ − a u ( τ ) + a e ( τ )] d τ
We can use the following approximation methods for the second term from D ( z ) D(z) D ( z ) D ( s ) D(s) D ( s )
D ( s ) D(s) D ( s ) rule z-transfer function D ( z ) D(z) D ( z ) approximation z-plane to s-plane stability a s + a \frac{a}{s+a} s + a a forward a ( z − 1 ) / T + a \frac{a}{(z-1)/T+a} ( z − 1 ) / T + a a s ← z − 1 T s \gets \frac{z-1}{T} s ← T z − 1 z ← s T + 1 z \gets sT + 1 z ← s T + 1 discrete → \to → a s + a \frac{a}{s+a} s + a a backward a ( z − 1 ) / ( T z ) + a \frac{a}{(z-1)/(Tz)+a} ( z − 1 ) / ( T z ) + a a s ← z − 1 T z s \gets \frac{z-1}{Tz} s ← T z z − 1 z ← 1 1 − T s z \gets \frac{1}{1-Ts} z ← 1 − T s 1 discrete ← \gets ← a s + a \frac{a}{s+a} s + a a trapzoid a ( 2 / T ) [ ( z − 1 ) / ( z + 1 ) ] + a \frac{a}{(2/T)[(z-1)/(z+1)]+a} ( 2/ T ) [( z − 1 ) / ( z + 1 )] + a a s ← 2 T z − 1 z + 1 s \gets \frac{2}{T} \frac{z-1}{z+1} s ← T 2 z + 1 z − 1 z ← 1 + T s / 2 1 − T s / 2 z \gets \frac{1+Ts/2}{1-Ts/2} z ← 1 − T s /2 1 + T s /2 discrete ↔ \leftrightarrow ↔