Given a homogeneous line $y = ax$ to a non-linear curve $f(x) = x^2 +1$ where $a,y,x \in \mathbb{R}$

assuming x are uniformly distributed on $[0,1]$. What is the value of a to minimize the squared error?

or we need to find

Or we can find the Jacobian $\mathcal{J}_f$

if $f = Ax$ then $\nabla_f = A$

or on-versus-all classification

idea: train $k$ different binary classifiers:

end-to-end version, or multi-class SVM with generalized Hinge loss:

type 1: false positive type 2: false negative

accuracy: $\frac{\text{TP + TN}}{\text{TP + TN + FP + FN}}$

precision is $\frac{\text{TP}}{\text{TP}+\text{FP}^{'}}$

recall is $\frac{\text{TP}}{\text{TP + FN}}$

• url: thoughts/.../probabilitics-modeling

probabilitic modeling

example: to assume each class is a Gaussian

discriminant analysis

$$P(x \mid y = 1, \mu_0, \mu_1, \beta) = \frac{1}{a_0} e^{-\|x-\mu_1\|^2_2}$$

maximum likelihood estimate

see also priori and posterior distribution

given $\Theta = \{\mu_1, \mu_2, \beta\}$:

$$\begin{aligned} \argmax_{\Theta} P(Z \mid \Theta) &= \argmax_{\Theta} \prod_{i=1}^{n} P(x^i, y^i \mid \Theta) \\ \end{aligned}$$

How can we predict the label of a new test point?

Or in another words, how can we run inference?

Check $\frac{P(y=0 \mid X, \Theta)}{P(y=1 \mid X, \Theta)} \ge 1$

Generalization for correlated features

Gaussian for correlated features:

$$\mathcal{N}(x \mid \mu, \Sigma) = \frac{1}{(2 \pi)^{d/2}|\Sigma|^{1/2}} \exp (-\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu))$$

Naive Bayes Classifier

assumption

Given the label, the coordinates are statistically independent

$$P(x \mid y = k, \Theta) = \pi_j P(x_j \mid y=k, \Theta)$$

idea: comparison between discriminative and generative models

• url: thoughts/Logistic-regression

Logistic regression

😄 fun fact: actually better for classification instead of regression problems

Assume there is a plane in $\mathbb{R}^d$ parameterized by $W$

$$\begin{aligned} P(Y = 1 \mid x, W) &= \phi (W^T x) \\ P(Y= 0 \mid x, W) &= 1 - \phi (W^T x) \\[12pt] &\because \phi (a) = \frac{1}{1+e^{-a}} \end{aligned}$$

maximum likelihood

$$1 - \phi (a) = \phi (-a)$$ $$\begin{aligned} W^{\text{ML}} &= \argmax_{W} \prod P(x^i, y^i \mid W) \\ &= \argmax_{W} \prod \frac{P(x^i, y^i, W)}{P(W)} \\ &= \argmax_{W} \prod P(y^i | x^i, W) P(x^i) \\ &= \argmax_{W} \lbrack \prod P(x^i) \rbrack \lbrack \prod P(y^i \mid x^i, W) \rbrack \\ &= \argmax_{W} \sum_{i=1}^{n} \log (\tau (y^i W^T x^i)) \end{aligned}$$

equivalent form

maximize the following:

$$\sum_{i=1}^{n} (y^i \log p^i + (1-y^i) \log (1-p^i))$$

• url: thoughts/optimization
• description: softmax

softmax

$$\text{softmax(y)}_i = \frac{e^{y_i}}{\sum_{i} e^{y_i}}$$

where $y \in \mathbb{R}^k$

Lien vers l'original

• url: thoughts/cross-entropy

cross entropy

Lien vers l'original

Lien vers l'original

Lien vers l'original

• url: thoughts/Logistic-regression

Logistic regression

😄 fun fact: actually better for classification instead of regression problems

Assume there is a plane in $\mathbb{R}^d$ parameterized by $W$

$$\begin{aligned} P(Y = 1 \mid x, W) &= \phi (W^T x) \\ P(Y= 0 \mid x, W) &= 1 - \phi (W^T x) \\[12pt] &\because \phi (a) = \frac{1}{1+e^{-a}} \end{aligned}$$

maximum likelihood

$$1 - \phi (a) = \phi (-a)$$ $$\begin{aligned} W^{\text{ML}} &= \argmax_{W} \prod P(x^i, y^i \mid W) \\ &= \argmax_{W} \prod \frac{P(x^i, y^i, W)}{P(W)} \\ &= \argmax_{W} \prod P(y^i | x^i, W) P(x^i) \\ &= \argmax_{W} \lbrack \prod P(x^i) \rbrack \lbrack \prod P(y^i \mid x^i, W) \rbrack \\ &= \argmax_{W} \sum_{i=1}^{n} \log (\tau (y^i W^T x^i)) \end{aligned}$$

equivalent form

maximize the following:

$$\sum_{i=1}^{n} (y^i \log p^i + (1-y^i) \log (1-p^i))$$

• url: thoughts/optimization
• description: softmax

softmax

$$\text{softmax(y)}_i = \frac{e^{y_i}}{\sum_{i} e^{y_i}}$$

where $y \in \mathbb{R}^k$

Lien vers l'original

• url: thoughts/cross-entropy

cross entropy

Lien vers l'original

Lien vers l'original

• url: thoughts/FFN

feed-forward neural network

stateless, and usually have no feedback loop.

universal approximation theorem

see also pdf (Cybenko, 1989)

idea: a single sigmoid activation functions in FFN can approximate closely any given probability distributions.

regression

Think of just a linear layers with some activation functions

import torch.optim as optim
import torch.nn as nn
 
class LinearRegression(nn.Module):
  def __init__(self, input_dim, output_dim):
    super().__init__()
    self.fc = nn.Linear(input_dim, output_dim)
  def forward(self, x): return self.fc(x)
 
model = LinearRegression(224, 10)
loss = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.005)
 
for ep in range(10):
  y_pred = model(X)
  l = loss(Y, y_pred)
  l.backward()
  optimizer.setp()
  optimzer.zero_grad()

classification

Think of one-hot encoding (binary or multiclass) cases

backpropagation

context: using SGD we can compute the gradient:

$$\nabla_W(L(w,b)) = \sum_{i} \nabla_W (l(f_{w,b}(x^i), y^i))$$

This is expensive, given that for deep model this is repetitive!

intuition: we want to minimize the error and optimized the saved weights learned through one forward pass.

vanishing gradient

happens in deeper network wrt the partial derivatives

because we applies the chain rule and propagating error signals backward from the output layer through all the hidden layers to the input, in very deep networks, this involves successive multiplication of gradients from each layer.

thus the saturated neurons $\sigma^{'}(x) \approx 0$, thus gradient does not reach the first layers.

solution:

• we can probably use activation functions (Leaky ReLU)
• better initialisation
• residual network

• url: thoughts/regularization

regularization

usually prone to overfitting given they are often over-parameterized

1. We can usually add regularization terms to the objective functions
2. Early stopping
3. Adding noise
4. structural regularization, via adding dropout

dropout

a case of structural regularization

a technique of randomly drop each node with probability $p$

Lien vers l'original

Bibliographie

• Novikoff, A. B. J. (1962). On Convergence Proofs for Perceptrons. Proceedings of the Symposium on the Mathematical Theory of Automata, 12, 615–622. https://apps.dtic.mil/sti/tr/pdf/AD0298258.pdf
• Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems, 2(4), 303–314.

Lien vers l'original

• url: thoughts/regularization

regularization

usually prone to overfitting given they are often over-parameterized

1. We can usually add regularization terms to the objective functions
2. Early stopping
3. Adding noise
4. structural regularization, via adding dropout

dropout

a case of structural regularization

a technique of randomly drop each node with probability $p$

Lien vers l'original

• url: thoughts/.../Convolutional-Neural-Network

Convolutional Neural Network

See also: this one assignment on CNN

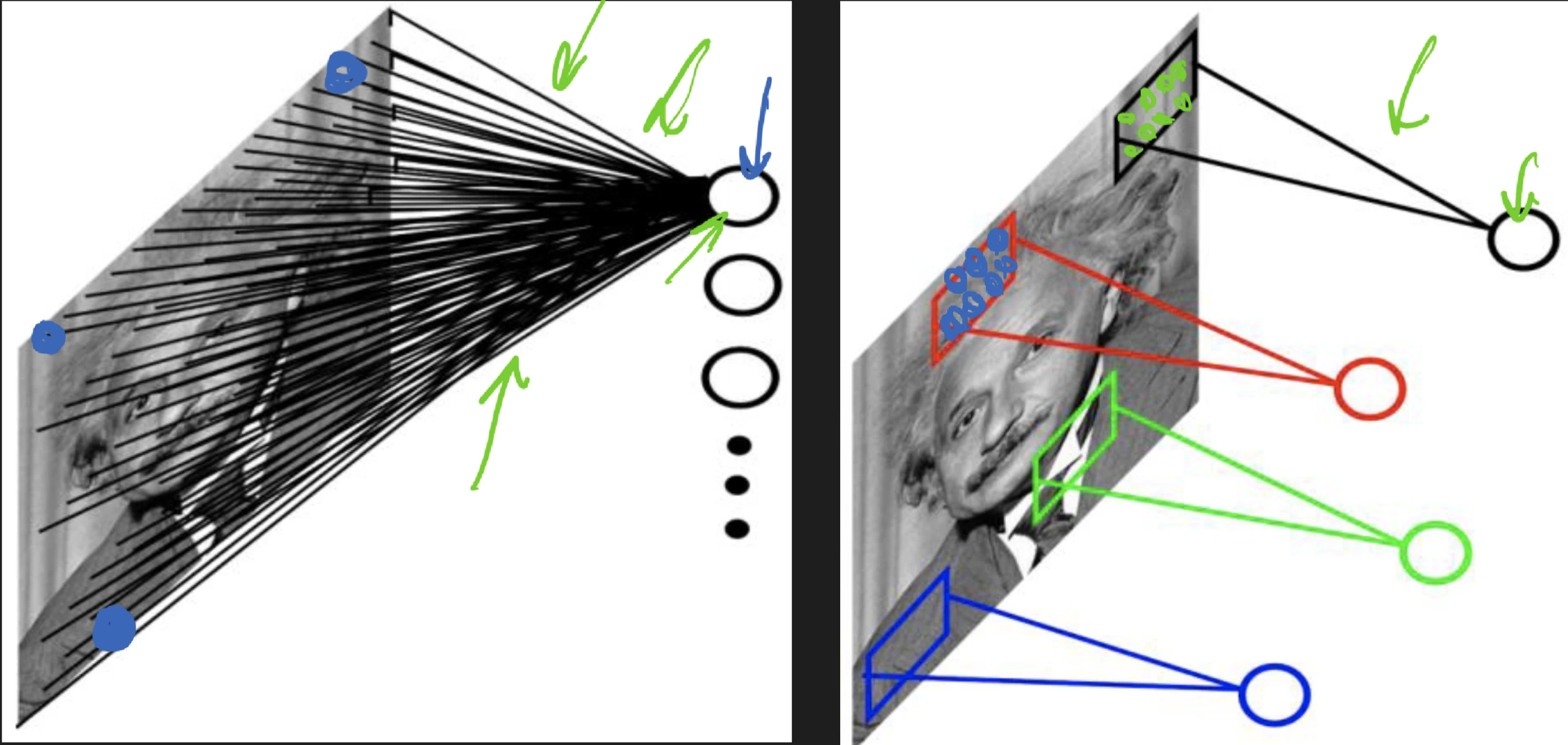
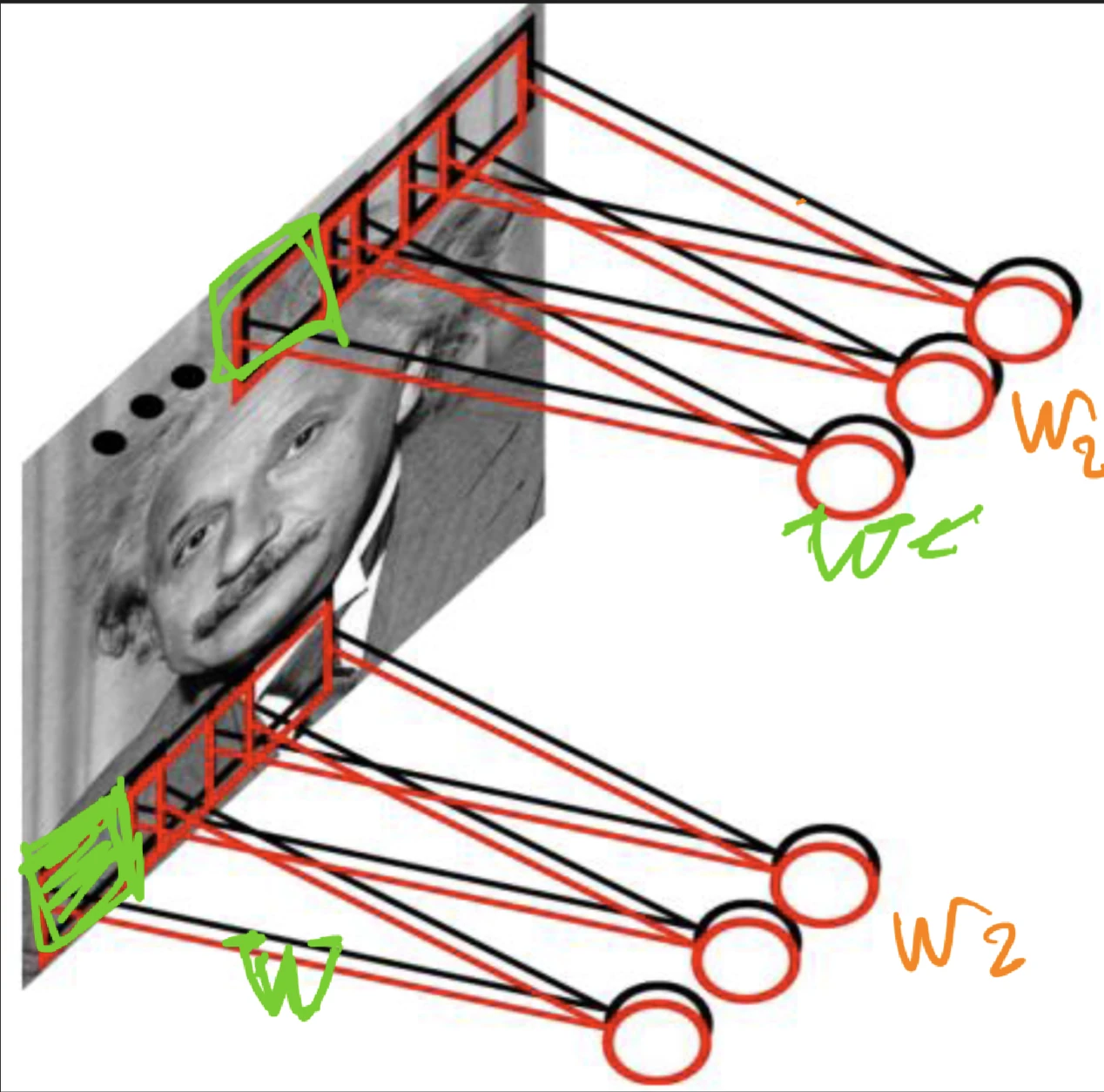
how can we exploit sparsity and locality?

think of sparse connectivity rather than full connectivity

where we exploiting invariance, it might be useful in other parts of the image as well

convolution

accept volume of size $W_1 \times H_1 \times D_1$ with four hyperparameters

• filters $K$
• spatial extent $F$
• stride $S$
• amount of zero padding $P$

calculation

produces a volume of size $W_2 \times H_2 \times D_2$ where:

• $W_2 = \frac{W_1 - F + 2P}{S} + 1$
• $H_2 = \frac{H_1 - F + 2P}{S} + 1$
• $D_2 = K$

1D convolution:

$$\begin{aligned} y &= (x*w) \\ y(i) &= \sum_{t}x(t)w(i-t) \end{aligned}$$

2D convolution:

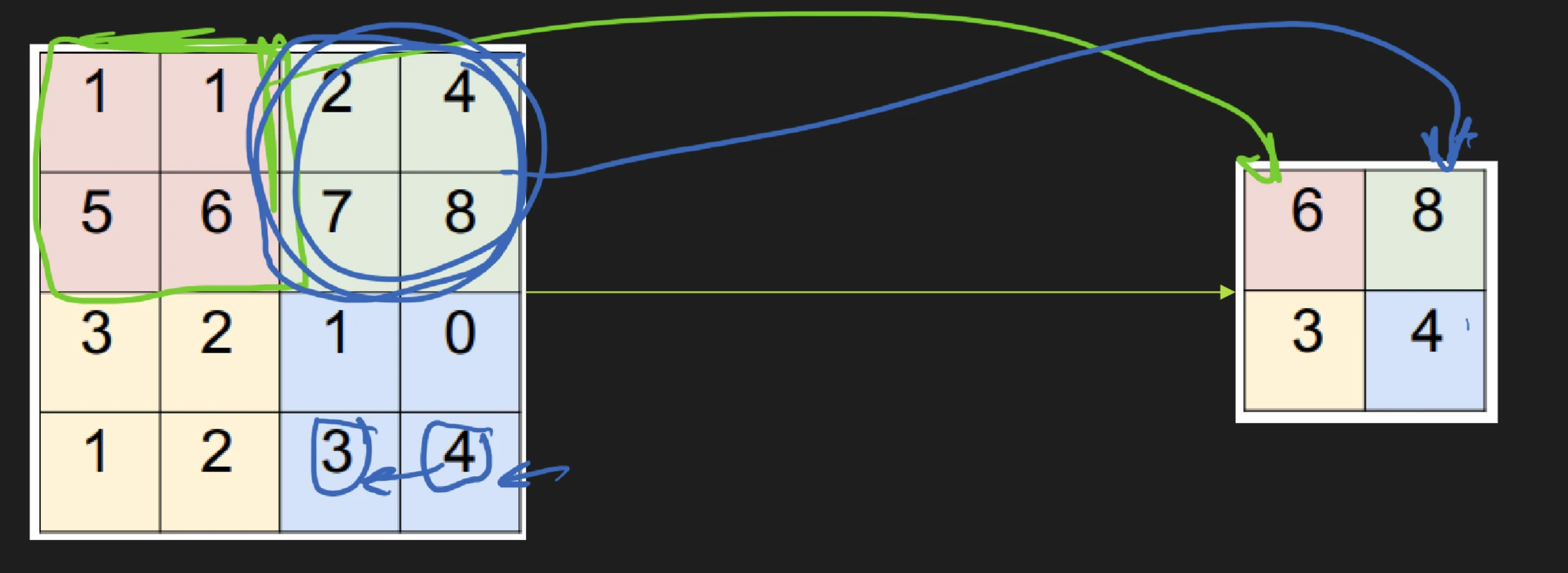
$$\begin{aligned} y &= (x*w) \\ y(i,j) &= \sum_{t_1} \sum_{t_2} x(t_1, t_2) w(i-t_1,j-t_2) \end{aligned}$$

max pooling

idea to reduce number of parameters

batchnorm

$$x^{j} = [x_1^j,\ldots,x_d^j]$$

Batch $X = [(x^1)^T \ldots (x^b)^T]^T$

Lien vers l'original

• url: thoughts/autoencoders

autoencoders

Think of using autoencoders to extract representations.

sparsity allows us to interpret hidden layers and internal representations of Transformers model.

graph TD
    A[Input X] --> B[Layer 1]
    B --> C[Layer 2]
    C --> D[Latent Features Z]
    D --> E[Layer 3]
    E --> F[Layer 4]
    F --> G[Output X']

    subgraph Encoder
        A --> B --> C
    end

    subgraph Decoder
        E --> F
    end

    style D fill:#c9a2d8,stroke:#000,stroke-width:2px,color:#fff
    style A fill:#98FB98,stroke:#000,stroke-width:2px
    style G fill:#F4A460,stroke:#000,stroke-width:2px

see also latent space

definition

$$\begin{aligned} \text{Enc}_{\Theta_1}&: \mathbb{R}^d \to \mathbb{R}^q \\ \text{Dec}_{\Theta_2}&: \mathbb{R}^q \to \mathbb{R}^d \\[12pt] &\because q \ll d \end{aligned}$$

loss function: $l(x) = \|\text{Dec}_{\Theta_2}(\text{Enc}_{\Theta_1}(x)) - x\|$

• url: thoughts/contrastive-representation-learning
• description: contrastive learning

contrastive representation learning

The goal of contrastive representation learning is to learn such an embedding space in which similar sample pairs stay close to each other while dissimilar ones are far apart. Contrastive learning can be applied to both supervised and unsupervised settings. article

intuition: to give a positive and negative pairs for optimizing loss function.

Lien vers l'original

training objective

we want smaller reconstruction error, or

$$\|\text{Dec}(\text{Sampler}(\text{Enc}(x))) - x\|_2^2$$

we want to get the latent space distribution to look something similar to isotopic Gaussian!

• url: thoughts/Kullback-Leibler-divergence
• description: KL divergence

Kullback-Leibler divergence

denoted as $D_{\text{KL}}(P \parallel Q)$

definition

The statistical distance between a model probability distribution $Q$ difference from a true probability distribution $P$:

$$D_{\text{KL}}(P \parallel Q) = \sum_{x \in \mathcal{X}} P(x) \log (\frac{P(x)}{Q(x)})$$

alternative form:

$$\begin{aligned} \text{KL}(p \parallel q) &= E_{x \sim p}(\log \frac{p(x)}{q(x)}) \\ &= \int_x P(x) \log \frac{p(x)}{q(x)} dx \end{aligned}$$Lien vers l'original

variational autoencoders

idea: to add a gaussian sampler after calculating latent space.

objective function:

$$\min (\sum_{x} \|\text{Dec}(\text{Sampler}(\text{Enc}(x))) - x\|^2_2 + \lambda \sum_{i=1}^{q}(-\log (\sigma_i^2) + \sigma_i^2 + \mu_i^2))$$Lien vers l'original

• url: thoughts/ensemble-learning

ensemble learning

idea: train multiple classifier and then combine them to improve performance.

aggregate their decisions via voting procedure.

Think of boosting, decision tree.

bagging

using non-overlapping training subset creates truly independent/diverse classifiers

bagging is essentially bootstrap aggregating where we do random sampling with replacement.

random forests

bagging but with random subspace methods ²

decision tree

• handle categorical features

NOTE

can overfit easily with deeper tree.

boosting

a greedier approach for reducing bias where we “pick base classifiers incrementally”.

we will train “weaker learner” and thus it can combined to become “stronger learner”.

Remarque

1. note that we can also write $a^T \phi$ where $\phi = [\phi(x^1),\ldots,\phi(x^n)]^T$ ↩

2. The idea of training each classifier using a random subset of the feature sets. Also known as feature bagging ↩

Lien vers l'original

• url: thoughts/Vapnik-Chrvonenkis-dimension

Vapnik-Chrvonenkis dimension

fancy name for the measure of size, or the cardinality of the largest sets of points that the algorithm can shatter.

definition

Let $H$ be a set set family and $C$ a set. Thus, their intersection is defined as the following set:

$$H \cap C \coloneqq \{h \cap C \mid h \in H\}$$

We say that set $C$ is shattered by $H$ if $H \cap C$ contains all the subsets of C, or:

$$|H \cap C| = 2^{|C|}$$

Thus, the VC dimension $D$ of $H$ is the cardinality of the largest set that is shattered by $H$.

Note that if arbitrary larget sets can be shattered, then the VC dimension is $\infty$

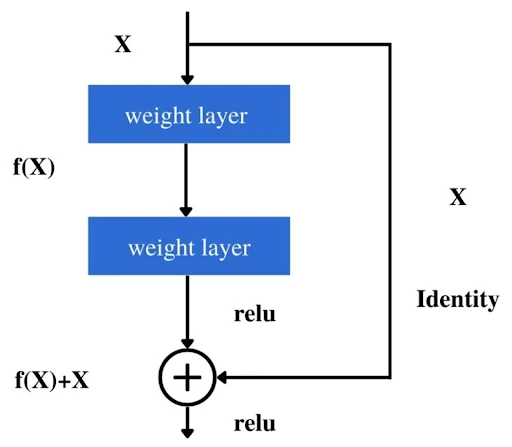Lien vers l'original